[next] [prev] [prev-tail] [tail] [up]

Chapter 14
Fractional Numbers

So far in this book we have used only integers for numerical values. In this chapter you will see two methods for storing fractional values — fixed point and floating point. Storing numbers in fixed point format requires that the programmer keep track of the location of the binary point1 within the bits allocated for storage. In the floating point format, the number is essentially written in scientific format and both the significand2 and exponent are stored.

14.1 Fractions in Binary

Before discussing the storage formats, we need to think about how fractional values are stored in binary. The concept is quite simple. We can extend Equation 2.6:

N = dn−1 × 2n−1 + dn−2 × 2n−2 + ...+d1 × 21 + d0 × 20 + d−1 ×2− 1 + d−2 × 2−2 +...
(14.1)

For example,

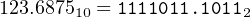123.687510 = 1111011.10112

because

d−1 × 2−1 = 1× 0.5
d−2 × 2−2 = 0× 0.25
d−3 × 2−3 = 1× 0.125
d−4 × 2−4 = 1× 0.0625

and thus

0.10112 = 0.510 + 0.12510 + 0.062510
= 0.687510 (14.2)

See Exercise 14-1 for an algorithm to convert decimal fractions to binary. We assume that you can convert the integral part and that Equation 14.1 is sufficient for converting from binary to decimal.

Although any integer can be represented as a sum of powers of two, an exact representation of fractional values in binary is limited to sums of inverse powers of two. For example, consider an 8-bit representation of the fractional value 0.9. From

0.111001102 = 0.8984375010
0.111001112 = 0.9023437510

we can see that

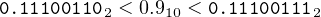0.111001102 < 0.910 < 0.111001112
(14.3)

In fact,

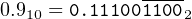----- 0.910 = 0.1110011002
(14.4)

where 1100 means that this bit pattern repeats forever.

Rounding off fractional values in binary is very simple. If the next bit to the right is one, add one to the bit position where rounding off. In the above example, we are rounding off to eight bits. The ninth bit to the right of the binary point is zero, so we do not add one in the eighth bit position. Thus, we use

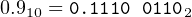0.910 = 0.1110 01102
(14.5)

which gives a round off error of

0.910 −0.111001102 = 0.910 − 0.898437510
= 0.001562510 (14.6)

We note here that two’s complement also works correctly for storing negative fractional values. You are asked to show this in Exercise 14-2.

14.2 Fixed Point ints

In a fixed point format, the storage area is divided into the integral part and the fractional part. The programmer must keep track of where the binary point is located. For example, we may decide to divide a 32-bit int in half and use the high-order 16 bits for the integral part and the low-order 16 bits for the fractional part.

My bank provides me with printed deposit slips that use this method. There are seven boxes for numerals. There is also a decimal point printed just to the left of the rightmost two boxes. Note that the decimal point does not occupy a box. That is, there are no digits allocated for the decimal point. So the bank assumes up to five decimal digits for the “dollars” part (rather optimistic), and the rightmost two decimal digits represent the “cents” part. The bank’s printing tells me how they have allocated the digits, but it is my responsibility to keep track of the location of the decimal point when filling in the digits.

One advantage of a fixed point format is that integer instructions can be used for arithmetic computations. Of course, the programmer must be very careful to keep track of which bits are allocated for the integral part and which for the fractional part. And the range of possible values is restricted by the number of bits.

An example of using ints for fixed point addition is shown in Listing 14.1.

 
1/* 
2 * rulerAdd.c 
3 * Adds two ruler measurements, to nearest 1/16th inch. 
4 * Bob Plantz - 18 June 2009 
5 */ 
6#include <stdio.h> 
7 
8int main(void) 
9{ 
10    int x, y, fraction_part, sum; 
11 
12    printf("Enter first measurement, inches: "); 
13    scanf("%d", &x); 
14    x = x << 4;         /* shift to integral part of variable */ 
15    printf("                     sixteenths: "); 
16    scanf("%d", &fraction_part); 
17    x = x | (0xf & fraction_part);  /* add in fractional part */ 
18 
19    printf("Enter second measurement, inches: "); 
20    scanf("%d", &y); 
21    y = y << 4;         /* shift to integral part of variable */ 
22    printf("                      sixteenths: "); 
23    scanf("%d", &fraction_part); 
24    y = y | (0xf & fraction_part);  /* add in fractional part */ 
25 
26    sum = x + y; 
27    printf("Their sum is %d and %d/16 inches\n", 
28          (sum >> 4), (sum & 0xf)); 
29 
30    return 0; 
31}
Listing 14.1: Fixed point addition. The high-order 28 bits are used for the integral part, the low-order 4 for the fractional part.)

The numbers are input to the nearest 1/16th inch, so the programmer has allocated four bits for the fractional part. This leaves 28 bits for the integral part. After the integral part is read, the stored number must be shifted four bit positions to the left to put it in the high-order 28 bits. Then the fractional part (in number of sixteenths) is added into the low-order four bits with a simple bit-wise or operation. Printing the answer also requires some bit shifting and some masking to filter out the fractional part.

This is clearly a contrived example. A program using floats would work just as well and be somewhat easier to write. However, the program in Listing 14.1 uses integer instructions, which execute faster than floating point. The hardware issues have become less significant in recent times. Modern CPUs use various parallelization schemes such that a mix of floating point and integer instructions may actually execute faster than only integer instructions. Fixed point arithmetic is often used in embedded applications where the CPU is small and may not have floating point capabilities.

14.3 Floating Point Format

The most important concept in this section is that floating point numbers are not real numbers.3 Real numbers include the continuum of all numbers from −∞ to +∞. You already understand that computers are finite, so there is certainly a limit on the largest values that can be represented. But the problem is much worse than simply a size limit.

As you will see in this section, floating point numbers comprise a very small subset of real numbers. There are significant gaps between adjacent floating point numbers. These gaps can produce the following types of errors:

To make matters worse, these errors can occur in intermediate results, where they are very difficult to debug.

The idea behind floating point formats is to think of numbers written in scientific format. This notation requires two numbers to completely specify a value — a significand and an exponent. To review, a decimal number is written in scientific notation as a significand times ten raised to an exponent. For example,

1,024 = 1.024 × 103 (14.7)
− 0.000089372 = −8.9372 × 10−5 (14.8)

Notice that the number is normalized such that only one digit appears to the left of the decimal point. The exponent of 10 is adjusted accordingly.

If we agree that each number is normalized and that we are working in base 10, then each floating point number is completely specified by three items:

  1. The significand.
  2. The exponent.
  3. The sign.

That is, in the above examples

The advantage of using a floating point format is that, for a given number of digits, we can represent a larger range of values. To illustrate this, consider a four-digit, unsigned decimal system. The range of integers that could be represented is

0 ≤ N ≤ 9999

Now, let’s allocate two digits for the significand and two for the exponent. We will restrict our scheme to unsigned numbers, but we will allow negative exponents. So we will need to use one of the exponent digits to store the sign of the exponent. We will use 0 for positive and 1 for negative. For example, 3.9 × 10−4 would be stored

PICT

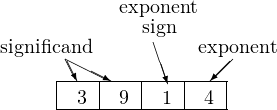
where each box holds one decimal digit. Some other examples are:

1000 represents 1.0 × 100
3702 represents 3.7 × 102
9316 represents 9.3 × 10−6

Our normalization scheme requires that there be a single non-zero digit to the left of the decimal point. We should also allow the special case of 0.0:

0000 represents 0.0

A little thought shows that this scheme allows numbers in the range

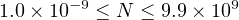1.0× 10−9 ≤ N ≤ 9.9× 109

That is, we have increased the range of possible values by a factor of 1014! However, it is important to realize that in both storage schemes, the integer and the floating point, we have exactly the same number of possible values — 104.

Although floating point formats can provide a much greater range of numbers, the distance between any two adjacent numbers depends upon the value of the exponent. Thus, floating point is generally less accurate than an integer representation, especially for large numbers.

To see how this works, let’s look at a plot of numbers (using our current scheme) in the range

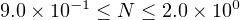9.0× 10−1 ≤ N ≤ 2.0× 100

PICT

Notice that the larger numbers are further apart than the smaller ones. (See Exercise 14-7 after you read Section 14.4.)

Let us pick some numbers from this range and perform some addition.

9111 represents 9.1 × 10−1
9311 represents 9.3 × 10−1

If we add these values, we get 0.91 + 0.93 = 1.84. Now we need to round off our “paper” addition in order to fit this result into our current floating point scheme:

1800 represents 1.8 × 100

On the other hand,

9411 represents 9.4 × 10−1
9311 represents 9.3 × 10−1

and adding these values, we get 0.94 + 0.93 = 1.87. Rounding off, we get:

1900 represents 1.9 × 100

So we see that starting with two values expressed to the nearest 1/100th, their sum is accurate only to the nearest 1/10.

To compare this with fixed point arithmetic, we could use the same four digits to store 0.93 this way

PICT

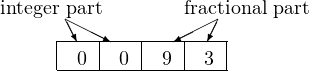
It is clear that this storage scheme allows us to perform both additions (0.91 + 0.93 and 0.94 + 0.93) and store the results exactly.

These round off errors must be taken into account when performing floating point arithmetic. In particular, the errors can occur in intermediate results when doing even moderately complex computations, where they are very difficult to detect.

14.4 IEEE 754

Specific floating point formats involve trade-offs between re4solution, round off errors, size, and range. The most commonly used formats are the IEEE 754.4 They range in size from four to sixteen bytes. The most common sizes used in C/C++ are floats (4 bytes) and doubles (8 bytes). The x86 processor performs floating point computations using an extended 10-byte format. The results are rounded to 4-byte mode if the programmer uses the float data type or 8-byte mode for the double data type.

In the IEEE 754 4-byte format, one bit is used for the sign, eight for the exponent, and twenty-three for the significand. The IEEE 754 8-byte format specifies one bit for the sign, eleven for the exponent, and fifty-two for the significand.

In this section we describe the 4-byte format in order to save ourselves (hand) computation effort. The goal is to get a feel for the limitations of floating point formats. The normalized form of the number in binary is given by Equation 14.9.

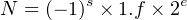N = (− 1)s × 1.f × 2e
(14.9)

where: s is the sign bit
f is the 23-bit fractional part
e is the 8-bit exponent

The bit patterns for floats and doubles are arranged as shown in Figure 14.1.

PICT

Figure 14.1: IEEE 754 bit patterns. (a) Float. (b) Double.

As in decimal, the exponent is adjusted such that there is only one non-zero digit to the left of the binary point. In binary, though, this digit is always one. Since it is always one, it need not be stored. Only the fractional part of the normalized value needs to be stored as the significand. This adds one bit to the significance of the fractional part. The integer part (one) that is not stored is sometimes called the hidden bit.

The sign bit, s, refers to the number. Another mechanism is used to represent the sign of the exponent, e. Your first thought is probably to use two’s complement. However, the IEEE format was developed in the 1970s, when floating point computations took a lot of CPU time. Many algorithms depend upon only the comparison of two numbers, and the computer scientists of the day realized that a format that allowed integer comparison instructions would result in faster execution times. So they decided to store a biased exponent as an unsigned int. The amount of the bias is one-half the range allocated for the exponent. In the case of an 8-bit exponent, the bias amount is 127.

Example 14-a ____________________________________________________________________________________________________

Show how 97.8125 is stored in 32-bit IEEE 754 binary format.

Solution:

First, convert the number to binary.

97.812510 = 1100001.11012
= (−1)0 ×1100001.1101× 20

Adjust the exponent to obtain the normalized form.

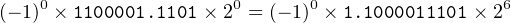(− 1)0 × 1100001.1101 × 20 = (− 1)0 × 1.1000011101× 26

Compute s, e+127, and f.

s = 0
e + 127 = 6 + 127
= 133
= 100001012
f = 10000111010000000000000

Finally, use Figure 14.1 to place the bit patterns. (Remember that the hidden bit is not stored; it is understood to be there.)

97.8125 is stored as 0 10000101 100001110100000000000002
or 42c3a00016
_______________________________________________________________________________□

Example 14-b ____________________________________________________________________________________________________

Using IEEE 754 32-bit format, what decimal number does the bit pattern 3e40000016 represent?

Solution:

First, convert the hexadecimal to binary, using spaces suggested by Figure 14.1.

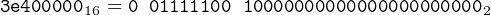3e400000 = 0 01111100 10000000000000000000000 16 2

Now compute the values of s, e, and f.

s = 0
e + 127 = 011111002
= 12410
e = −310
f = 10000000000000000000000

Finally, plug these values into Equation 14.9. (Remember to add the hidden bit.)

(−1)0 ×1.100…00× 2−3 = (−1)0 ×0.0011× 20
= 0.187510
__________________________________________________________________________________________________________________________________________________________□

Example 14-c ____________________________________________________________________________________________________

Using IEEE 754 32-bit format, what decimal number would the bit pattern 0000000016 represent? (The specification states that it is an exception to the format and is defined to represent 0.0. This example provides some motivation for this exception.)

Solution:

The conversion to binary is trivial. Computing the values of s, e, and f.

s = 0
e + 127 = 000000002
e = −12710
f = 00000000000000000000000

Finally, plug these values into Equation 14.9. (Remember to add the hidden bit.)

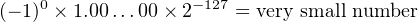(− 1)0 × 1.00...00× 2−127 = very small number

__________________________________________________________________________________□

This last example illustrates a problem with the hidden bit — there is no way to represent zero. To address this issue, the IEEE 754 standard has several special cases.

14.5 Floating Point Hardware

Until the introduction of the Intel 486DX in4 April 1989, the x87 Floating Point Unit was on a separate chip. It is now included on the CPU chip although it uses a somewhat different execution architecture than the Integer Unit in the CPU.

In 1997 Intel added MMX™(Multimedia Extensions) to their processors, which includes instructions that process multiple data values with a single instruction (SIMD). Operations on single data items are called scalar operations, while those on multiple data items in parallel are called vector operations. Vector operations are useful for many multi-media and scientific applications. In this book we will discuss only scalar floating point operations. Originally, MMX only performed integer computations. But in 1998 AMD added the 3DNow!™extension to MMX, which includes floating point instructions. Intel soon followed suit.

Intel then introduced SSE (Streaming SIMD Extension) on the Pentium III in 1999. Several versions have evolved over the years — SSE, SSE2, SSE3, and SSE4A — as of this writing. There are instructions for performing both integer and floating point operations on both scalar and vector values.

The x86-64 architecture includes three sets of instructions for working with floating point values:

All three floating point instruction sets include a wide variety of instructions to perform the following operations:

In addition, the x87 includes instructions for transcendental functions — sine, cosine, tangent, and arc tangent, and logarithm functions.

We will not cover all the instructions in this book. The following subsections provide an introduction to how each of the three sets of instructions is used. See the manuals [2] – [6] and [14] – [18] for details.

14.5.1 SSE2 Floating Point

Most of the SSE2 instructions operate on multiple data items simultaneously — single instruction, multiple data (SIMD). There are SSE2 instructions for both integer and floating point operations. Integer instructions operate on up to sixteen 8-bit, eight 16-bit, four 32-bit, two 64-bit, or one 128-bit integers at a time. Vector floating point instructions operate on all four 32-bit or both 64-bit floats in a register simultaneously. Each data item is treated independently. These instructions are useful for algorithms that do things like process arrays. One SSE2 instruction can operate on several array elements in parallel, resulting in considerable speed gains. Such algorithms are common in multi-media and scientific applications.

In this book we will only consider some of the scalar floating-point instructions, which operate on only single data items. The SSE2 instructions are the preferred floating-point implementation in 64-bit mode. These instructions operate on either 32-bit (single-precision) or 64-bit (double-precision) values. The scalar instructions operate on only the low-order portion of the 128-bit xmm registers, with the high-order 64 or 96 bits remaining unchanged.

SSE includes a 32-bit MXCSR register that has flags for handling floating-point arithmetic errors. These flags are shown in Table 14.1.

bits mnemonic meaning default
31 – 18 – reserved
17 MM Misaligned Exception Mask 0
16 – reserved
15 FZ Flush-toZero for Masked Underflow 0
14 – 13 RC Floating-Point Rounding Control 00
12 PM Precision Exception Mask 1
11 UM Underflow Exception Mask 1
10 OM Overflow Exception Mask 1
9 ZM Zero-Divide Exception Mask 1
8 DM Denormalized-Operand Exception Mask 1
7 IM Invalid-Operation Exception Mask 1
6 DAZ Denormals Are Zero 0
5 PE Precision Exception 0
4 UE Underflow Exception 4 0
3 OE Overflow Exception 0
2 ZE Zero-Divide Exception 1
1 DE Denormalized-Operand Exce4ption 0
0 IE Invalid-Operation Exception 0

Table 14.1: MXCSR status register.

SSE instructions that perform arithmetic operations and the SSE compare instructions also affect the status flags in the rflags register. Thus the regular conditional jump instructions (Section 10.1.2, page 676) are used to control program flow based on floating-point computations.

The instruction mnemonics used by the gnu assembler are mostly the same as given in the manuals, [2] – [6] and [14] – [18]. Since they are quite descriptive with respect to operand sizes, a size letter is not appended to the mnemonic, except when one of the operands is in memory and the size is ambiguous. Of course, the operand order used by the gnu assembler is still reversed compared to the manufacturers’ manuals, and the register names are prefixed with the “%” character.

A very important set of instructions provided for working with floating point values are those to convert between integer and floating point formats. The scalar conversion SSE2 instructions are shown in Table 14.2.

mnemonic source destination meaning
cvtsd2si xmm reg. 32-bit integer convert scalar 64-bit
or mem. reg. float to 32-bit integer
cvtsd2ss xmm reg. xmm reg. or convert scalar 64-bit
mem. float to 32-bit float
cvtsi2sd integer reg. xmm reg. convert 32-bit integer
or mem. to scalar 64-bit float
cvtsi2sdq integer reg. xmm reg. convert 64-bit integer
or mem. to scalar 64-bit float
cvtsi2ss integer reg. xmm reg. convert 32-bit integer
or mem. to scalar 32-bit float
cvtsi2ssq integer reg. xmm reg. convert 64-bit integer
or mem. to scalar 32-bit float
cvtss2sd xmm reg. another xmm reg. convert scalar 32-bit
or mem. float to 64-bit float
cvtss2si xmm reg. 32-bit integer convert scalar 32-bit
or mem. reg. float to 32-bit integer
cvtss2siq xmm reg. 64-bit integer convert scalar 32-bit
or mem. reg. float to 64-bit integer

Table 14.2: SSE scalar floating point conversion instructions. Source and destination xmm registers must be different. The low-order portion of the xmm register is used. When reading from or writing to memory, the “q” suffix is used to designate a 64-bit value.

Data movement and arithmetic instructions must distinguish between scalar and vector operations on values in the xmm registers. The low-order portion of the register is used for scalar operations. Vector operations are performed on multiple data values packed into a single register. See Table 14.3 for a sampling of SSE2 data movement and arithmetic instructions.

mnemonic source destination meaning
addps xmm reg. or mem. xmm reg. add packed 32-bit floats
addpd xmm reg. or mem. xmm reg. add packed 64-bit floats
addss xmm reg. or mem. xmm reg. add scalar 32-bit floats
addsd xmm reg. or mem. xmm reg. add scalar 64-bit floats
divps xmm reg. or mem. xmm reg. divide packed 32-bit floats
divpd xmm reg. or mem. xmm reg. divide packed 64-bit floats
divss xmm reg. or mem. xmm reg. divide scalar 32-bit floats
divsd xmm reg. or mem. xmm reg. divide scalar 64-bit floats
movss xmm reg. or mem. xmm reg. move scalar 32-bit float
movss xmm reg. xmm reg. or mem. move scalar 32-bit float
movsd xmm reg. or mem. xmm reg. move scalar 64-bit float
movsd xmm reg. xmm reg. or mem. move scalar 64-bit float
mulps xmm reg. or mem. xmm reg. multiply packed 32-bit floats
mulpd xmm reg. or mem. xmm reg. multiply packed 64-bit floats
mulss xmm reg. or mem. xmm reg. multiply scalar 32-bit floats
mulsd xmm reg. or mem. xmm reg. multiply scalar 64-bit floats
subps xmm reg. or mem. xmm reg. subtract packed 32-bit floats
subpd xmm reg. or mem. xmm reg. subtract packed 64-bit floats
subss xmm reg. or mem. xmm reg. subtract scalar 32-bit floats
subsd xmm reg. or mem. xmm reg. subtract scalar 64-bit floats

Table 14.3: Some SSE floating point arithmetic and data movement instructions. Source and destination xmm registers must be different. Scalar instructions use the low-order portion of the xmm registers.

Notice that the code for the basic operation is followed by a “p” or “s” for “packed” or “scalar.” This character is then followed by a “d” or “s” for “double” (64-bit) or “single” (32-bit) data item.

We will use the program in Listing 14.2 to illustrate a few floating point operations.

 
1/* 
2 * frac2float.c 
3 * Converts fraction to floating point. 
4 * Bob Plantz - 18 June 2009 
5 */ 
6 
7#include <stdio.h> 
8 
9int main(void) 
10{ 
11    int x, y; 
12    double z; 
13 
14    printf("Enter two integers: "); 
15    scanf("%i %i", &x, &y); 
16    z = (double)x / y; 
17    printf("%i / %i = %lf\n", x, y, z); 
18    return 0; 
19 }
Listing 14.2: Converting a fraction to a float.

Compiling this program in 64-bit mode produced the assembly language in Listing 14.3.

 
1        .file  "frac2float.c" 
2        .section      .rodata 
3.LC0: 
4        .string"Enter two integers: " 
5.LC1: 
6        .string"%i %i" 
7.LC2: 
8        .string"%i / %i = %lf\n" 
9        .text 
10        .globlmain 
11        .type  main, @function 
12main: 
13        pushq  %rbp 
14        movq  %rsp, %rbp 
15        subq  $32, %rsp 
16        movl  $.LC0, %edi 
17        movl  $0, %eax 
18        call  printf 
19        leaq  -12(%rbp), %rdx     # address of y 
20        leaq  -16(%rbp), %rax     # address of x 
21        movq  %rax, %rsi 
22        movl  $.LC1, %edi 
23        movl  $0, %eax            # no xmm arguments 
24        call  __isoc99_scanf 
25        movl  -16(%rbp), %eax     # load x 
26        cvtsi2sd      %eax, %xmm0 # convert to double 
27        movl  -12(%rbp), %eax     # load y 
28        cvtsi2sd      %eax, %xmm1 # convert to double 
29        divsd  %xmm1, %xmm0        # (double)x / (double)y 
30        movsd  %xmm0, -8(%rbp)     # store z 
31        movl  -12(%rbp), %edx     # load y 
32        movl  -16(%rbp), %ecx     # load x 
33        movq  -8(%rbp), %rax 
34        movq  %rax, -24(%rbp) 
35        movsd  -24(%rbp), %xmm0    # load z 
36        movl  %ecx, %esi          # x to correct register 
37        movl  $.LC2, %edi 
38        movl  $1, %eax            # one xmm argument (in xmm0) 
39        call  printf 
40        movl  $0, %eax 
41        leave 
42        ret 
43        .size  main, .-main 
44        .ident"GCC: (Ubuntu/Linaro 4.7.0-7ubuntu3) 4.7.0" 
45        .section      .note.GNU-stack,"",@progbits
Listing 14.3: Converting a fraction to a float (gcc assembly language, 64-bit).

Before the division is performed, both integers must be converted to floating point. This takes place on lines 25 – 28:

25        movl  -16(%rbp), %eax     # load x 
26        cvtsi2sd      %eax, %xmm0 # convert to double 
27        movl  -12(%rbp), %eax     # load y 
28        cvtsi2sd      %eax, %xmm1 # convert to double

The cvtsi2sd instruction on lines 26 and 28 converts a signed integer to a scalar double-precision floating point value. The signed integer can be either 32 or 64 bits and can be located in a general purpose register or in memory. The double-precision float will be stored in the low-order 64 bits of the specified xmmn register. The high-order 64 bits to the xmmn register are not changed.

The division on line 29 leaves the result in the low-order 64 bits of xmm0, which is then stored in z:

29        divsd  %xmm1, %xmm0        # (double)x / (double)y 
30        movsd  %xmm0, -8(%rbp)     # store z

The movapd instruction moves the entire 128 bits, and the movsd instruction moves only the low-order 64 bits.

The floating point arguments are passed in the registers xmm0, xmm1, …, xmm15 in left-to-right order. So the value of z is loaded into the (xmm0) register for passing to the printf function, and the number of floating point values passed to it must be stored in eax:

35        movsd  -24(%rbp), %xmm0    # load z 
36        movl  %ecx, %esi          # x to correct register 
37        movl  $.LC2, %edi 
38        movl  $1, %eax            # one xmm argument (in xmm0) 
39        call  printf

14.5.2 x87 Floating Point Unit

The x87 FPU has eight 80-bit data registers, its own status register, and its own stack pointer. Floating point values are stored in the floating point data registers in an extended format.:

So there are 64 bits (63 – 0) for the significand. Since there is no hidden bit in the extended format, one of these bits, bit 63, is required for the integer part.

Example 14-d ____________________________________________________________________________________________________

Show how 97.8125 is stored in 80-bit extended IEEE 754 binary format.

Solution:

First, convert the number to binary.

97.812510 = 1100001.11012
(−1)0 ×1100001.1101× 20

Adjust the exponent to obtain the normalized form.

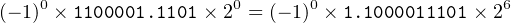(− 1)0 × 1100001.1101 × 20 = (− 1)0 × 1.1000011101× 26

Compute s, e+16383.

s = 0
e + 16383 = 6 + 16383
= 16389
= 1000000000001012

Filling in the bit patterns as specified above:

97.8125 is stored as 0 100000000000101 1 1000011101000000000000…02
or 4005c3a000000000000016

Compare this with the 32-bit format in Example 14-a above.

__________________________________________________________________________________□

The 16-bit Floating Point Unit Status Word register shows the results of floating point operations. The meaning of each bit is shown in Table 14.4.

bit number mnemonic meaning
0 IE invalid operation
1 DE denormalized operation
2 ZE zero divide
3 OE overflow
4 UE underflow
5 PE precision
6 SF stack fault
7 ES error summary status
8 C0 condition code 0
9 C1 condition code 1
10 C2 condition code 2
11 – 13 TOP top of stack
14 C3 condition code 3
15 B FPU busy

Table 14.4: x87 Status Word.

Figure 14.2 shows a pictorial representation of the x87 floating point registers. The absolute locations are named fpr0, fpr1,…,fpr7 in this figure.

PICT

Figure 14.2: x87 floating point register stack. The fpri represent the absolute locations. The st(j) are the stack names, which are used by the instructions. In this example the top of the stack is at fpr3, as shown in bits 13 – 11 of the x87 status register.

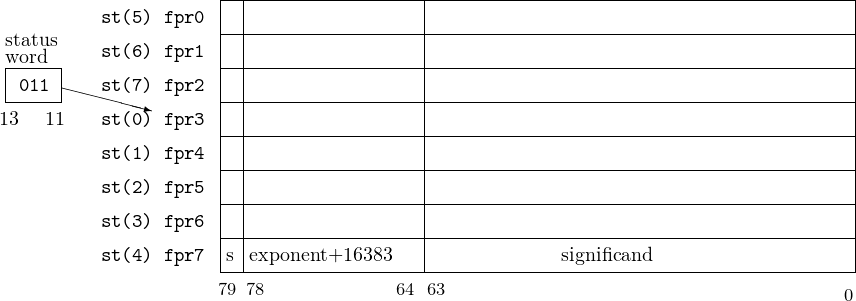
The floating point registers are accessed by program instructions as a stack with st(0) being the register at the top of the stack. It “grows” from higher number registers to lower. The TOP field (bits 13 – 11) in the FPU Status Word holds the (absolute) register number that is currently the top of the stack. If the stack is full, i.e., fpr0 is the top of the stack, a push causes the TOP field to roll over, and the next item goes into register fpr7. (The value that was in fpr7 is lost.)

The instructions that read data from memory automatically push the value onto the top of the register stack. Arithmetic instructions are provided that operate on the value(s) on the top of the stack. For example, the faddp instruction adds the two values on the top of the stack and leaves their sum on the top. The stack has one less value on it. The original two values are gone.

Many floating point instructions allow the programmer to access any of the floating point registers, %st(i), where i = 0…7, relative to the top of the stack. Fortunately, the programmer does not need to keep track of where the top is. When using this format, %st(i) refers to the ith register from the top of the stack. For example, if fpr3 is the current top of the stack, the instruction

        fadd    %st(2), %st(0)

will add the value in the fpr5 register to the value in the fpr3 register, leaving the result in the fpr3 register.

Table 14.5 provides some examples of the floating point instruction set. Notice that the instructions that deal only with the floating point register stack do not use the size suffix letter, s.

mnemonic source destination

meaning

fadds memfloat

add memfloat to st(0)

faddp

add st(0) to st(1) and pop register stack

fchs

change sign of st(0)

fcoms memfloat

compare st(0) with memfloat

fcomp

compare st(0) with st(1) and pop register stack

fcos

replace st(0) with its cosine

fdivs memfloat

divide st(0) by memfloat

fdivp

divide st(0) by st(1), store result in st(1), and pop register stack

filds memint

convert integer at memint to 80-bit float and push onto register stack

fists memint

convert 80-bit float at st(0) to int and store at memint

flds memfloat

convert float at memint to 80-bit float and push onto register stack

fmuls memfloat

multiply st(0) by memfloat

fmulp

multiply st(0) by st(1), store result in st(1), and pop register stack

fsin

replace st(0) with its sine

fsqrt

replace st(0) with its square root

fsts memint

convert 80-bit float at st(0) to s size float and store at memint

fsubs memfloat

subtract memfloat from st(0)

fsubp

subtract st(0) from st(1) and pop register stack

s = s, l, t

Table 14.5: A sampling of x87 floating point instructions. Size characters are: s = 32-bit, l = 64-bit, t = 80-bit.

To avoid ambiguity the gnu assembler requires a single letter suffix on the floating point instructions that access memory. The suffixes are:

’s’ for single precision – 32-bit
’l’ for long (or double) precision – 64-bit
’t’ for ten-byte – 80-bit

Most of the floating point instructions have several variants. See [2] – [6] and [14] – [18] for details. In general,

Compiling the fraction conversion program of Listing 14.2 in 32-bit mode shows (Listing 14.4) that the compiler uses the x87 floating-point instructions. This ensures backward compatibility since the x86-32 architecture does not need to include SSE instructions.

 
1        .file  "frac2float.c" 
2        .section      .rodata 
3.LC0: 
4        .string"Enter two integers: " 
5.LC1: 
6        .string"%i %i" 
7.LC2: 
8        .string"%i / %i = %lf\n" 
9        .text 
10        .globlmain 
11        .type  main, @function 
12main: 
13        pushl  %ebp 
14        movl  %esp, %ebp 
15        andl  $-16, %esp 
16        subl  $64, %esp 
17        movl  $.LC0, (%esp) 
18        call  printf 
19        leal  52(%esp), %eax   # address of x 
20        movl  %eax, 8(%esp) 
21        leal  48(%esp), %eax   # address of y 
22        movl  %eax, 4(%esp) 
23        movl  $.LC1, (%esp) 
24        call  __isoc99_scanf 
25        movl  48(%esp), %eax   # load y 
26        movl  %eax, 44(%esp)   # needs to be in memory to 
27        fildl  44(%esp)         # convert to 80-bit float and push 
28        movl  52(%esp), %eax   # load x 
29        movl  %eax, 44(%esp) 
30        fildl  44(%esp)         # convert to 80-bit float and push 
31        fdivrp%st, %st(1)       # (long double)x / (long double) y 
32        fstpl  56(%esp)         # store z 
33        movl  52(%esp), %edx   # load x 
34        movl  48(%esp), %eax   # load y 
35        fldl  56(%esp)         # load z 
36        fstpl  12(%esp)         # put z on call stack 
37        movl  %edx, 8(%esp)    # put x on call stack 
38        movl  %eax, 4(%esp)    # put y on call stack 
39        movl  $.LC2, (%esp) 
40        call  printf 
41        movl  $0, %eax 
42        leave 
43        ret 
44        .size  main, .-main 
45        .ident"GCC: (Ubuntu/Linaro 4.7.0-7ubuntu3) 4.7.0" 
46        .section      .note.GNU-stack,"",@progbits
Listing 14.4: Converting a fraction to a float (gcc assembly language, 32-bit).

We add comments to lines 19 and 21 to show where the x and y variables are located in the stack frame.

19        leal  52(%esp), %eax   # address of x 
20        movl  %eax, 8(%esp) 
21        leal  48(%esp), %eax   # address of y 
22        movl  %eax, 4(%esp) 
23        movl  $.LC1, (%esp) 
24        call  __isoc99_scanf

Rather than actually push the arguments onto the stack, enough space was allocated on the stack (line 15) to directly store the values in the location where they would be if they had been pushed there. This is more efficient that pushing each argument.

Casting an int to a float requires a conversion in the storage format. This conversion is done by the x87 FPU as an integer is pushed onto the floating point register stack using the fildl instruction. This conversion can only be done to an integer that is stored in memory. The compiler uses a location on the call stack to temporarily store each integer so it can be converted:

25        movl  48(%esp), %eax   # load y 
26        movl  %eax, 44(%esp)   # needs to be in memory to 
27        fildl  44(%esp)         # convert to 80-bit float and push 
28        movl  52(%esp), %eax   # load x 
29        movl  %eax, 44(%esp) 
30        fildl  44(%esp)         # convert to 80-bit float and push

Each of the fildl instructions on lines 27 and 30 converts a 32-bit integer to an 80-bit float and pushes the float onto the x87 register stack. At this point the floating-point equivalent of x is at the top of the stack, and the floating-point equivalent of y is immediately below it. Then the floating-point division instruction:

31        fdivrp%st, %st(1)       # (long double)x / (long double) y

divides the number at st(0) (the (0) can be omitted) by the number at st(1) and pops the x87 register stack so that the result is now at the top of the stack.

Finally, the fstpl instruction is used to pop the value off the top of the x87 register stack and store it in memory — at its proper location on the call stack. The “l” suffix indicates that 64 bits of memory should be used for storing the floating-point value. So the 80-bit value on the top of the x87 register stack is rounded to 64 bits as it is stored in memory. The other three arguments are also stored on the call stack.

32        fstpl  56(%esp)         # store z 
33        movl  52(%esp), %edx   # load x 
34        movl  48(%esp), %eax   # load y 
35        fldl  56(%esp)         # load z 
36        fstpl  12(%esp)         # put z on call stack 
37        movl  %edx, 8(%esp)    # put x on call stack 
38        movl  %eax, 4(%esp)    # put y on call stack

Note that the 32-bit version of printf does not receive arguments in registers, so eax is not used.

14.5.3 3DNow! Floating Point

The 3DNow! instructions use the low-order 64 bits in the same physical registers at the x87. These 64-bit portions are named mmx0, mmx1,…, mmx7. They are used as fixed register, not in a stack configuration. Execution of a 3DNow! instruction changes the TOP field (bits 13 – 11) in the MXCSR status register, so the top of stack is lost for any subsequent x87 instructions. The bottom line is that x87 and 3DNow! instructions cannot be used simultaneously.

Another limitation of the 3DNow! instructions set is that it only handles 32-bit floating point.

These limitations of the 3DNow! instruction set make it essentially obsolete in the x86-64 architecture, so it will not be discussed further in this book.

14.6 Comments About Numerical Accuracy

Beginning programmers often see floating point arithmetic as more accurate than integer. It is true that even adding two very large integers can cause overflow. Multiplication makes it even more likely that the result will be very large and, thus, overflow. And when used with two integers, the / operator in C/C++ causes the fractional part to be lost. However, as you have seen in this chapter, floating point representations have their own set of inaccuracies.

Arithmetically accurate results require a thorough analysis of your algorithm. Some points to consider:

14.7 Instructions Introduced Thus Far

This summary shows the assembly language instructions introduced thus far in the book. The page number where the instruction is explained in more detail, which may be in a subsequent chapter, is also given. This book provides only an introduction to the usage of each instruction. You need to consult the manuals ([2] – [6], [14] – [18]) in order to learn all the possible uses of the instructions.

14.7.1 Instructions

data movement:
opcode source destination action page
cbtw convert byte to word, al → ax 696
cwtl convert word to long, ax → eax 696
cltq convert long to quad, eax → rax 696
cwtd convert word to long, ax → dx:ax 786
cltd convert long to quad, eax → edx:eax 786
cqto convert quad to octuple, rax → rdx:rax 786
cmovcc %reg/mem %reg conditional move 706
movs $imm/%reg %reg/mem move 506
movs mem %reg move 506
movsss $imm/%reg %reg/mem move, sign extend 693
movzss $imm/%reg %reg/mem move, zero extend 693
popw %reg/mem pop from stack 566
pushw $imm/%reg/mem push onto stack 566
s = b, w, l, q; w = l, q; cc = condition codes

arithmetic/logic:
opcode source destination action page
adds $imm/%reg %reg/mem add 607
adds mem %reg add 607
ands $imm/%reg %reg/mem bit-wise and 747
ands mem %reg bit-wise and 747
cmps $imm/%reg %reg/mem compare 676
cmps mem %reg compare 676
decs %reg/mem decrement 699
divs %reg/mem unsigned divide 777
idivs %reg/mem signed divide 784
imuls %reg/mem signed multiply 775
incs %reg/mem increment 698
leaw mem %reg load effective address 579
muls %reg/mem unsigned multiply 769
negs %reg/mem negate 789
ors $imm/%reg %reg/mem bit-wise inclusive or 747
ors mem %reg bit-wise inclusive or 747
sals $imm/%cl %reg/mem shift arithmetic left 756
sars $imm/%cl %reg/mem shift arithmetic right 751
shls $imm/%cl %reg/mem shift left 756
shrs $imm/%cl %reg/mem shift right 751
subs $imm/%reg %reg/mem subtract 612
subs mem %reg subtract 612
tests $imm/%reg %reg/mem test bits 676
tests mem %reg test bits 676
xors $imm/%reg %reg/mem bit-wise exclusive or 747
xors mem %reg bit-wise exclusive or 747
s = b, w, l, q; w = l, q

program flow control:
opcode location action page
call label call function 546
ja label jump above (unsigned) 683
jae label jump above/equal (unsigned) 683
jb label jump below (unsigned) 683
jbe label jump below/equal (unsigned) 683
je label jump equal 679
jg label jump greater than (signed) 686
jge label jump greater than/equal (signed) 686
jl label jump less than (signed) 686
jle label jump less than/equal (signed) 686
jmp label jump 691
jne label jump not equal 679
jno label jump no overflow 679
jcc label jump on condition codes 679
leave undo stack frame 580
ret return from function 583
syscall call kernel function 587
cc = condition codes

x87 floating point:
opcode source destination action page
fadds memfloat add 859
faddp add/pop 859
fchs change sign 859
fcoms memfloat compare 859
fcomp compare/pop 859
fcos cosine 859
fdivs memfloat divide 859
fdivp divide/pop 859
filds memint load integer 859
fists memint store integer 859
flds memfloat load floating point 859
fmuls memfloat multiply 859
fmulp multiply/pop 859
fsin sine 859
fsqrt square root 859
fsts memint floating point store 859
fsubs memfloat subtract 859
fsubp subtract/pop 859
s = s, l, t

SSE floating point conversion:
opcode source destination action page
cvtsd2si %xmmreg/mem %reg scalar double to signed integer 845
cvtsd2ss %xmmreg %xmmreg/%reg scalar double to single float 845
cvtsi2sd %reg %xmmreg/mem signed integer to scalar double 845
cvtsi2sdq %reg %xmmreg/mem signed integer to scalar double 845
cvtsi2ss %reg %xmmreg/mem signed integer to scalar single 845
cvtsi2ssq %reg %xmmreg/mem signed integer to scalar single 845
cvtss2sd %xmmreg %xmmreg/mem scalar single to scalar double 845
cvtss2si %xmmreg/mem %reg scalar single to signed integer 845
cvtss2siq %xmmreg/mem %reg scalar single to signed integer 845

14.7.2 Addressing Modes

__________________________________________________________

register direct:

The data value is located in a CPU register.

syntax: name of the register with a “%” prefix.

example: movl    %eax, %ebx

immediate data:

The data value is located immediately after the instruction. Source operand only.

syntax: data value with a “$” prefix.

example: movl    $0xabcd1234, %ebx

base register plus offset:

The data value is located in memory. The address of the memory location is the sum of a value in a base register plus an offset value.

syntax: use the name of the register with parentheses around the name and the offset value immediately before the left parenthesis.

example: movl    $0xaabbccdd, 12(%eax)

rip-relative:

The target is a memory address determined by adding an offset to the current address in the rip register.

syntax: a programmer-defined label

example: je     somePlace

indexed:

The data value is located in memory. The address of the memory location is the sum of the value in the base_register plus scale times the value in the index_register, plus the offset.

syntax: place parentheses around the comma separated list (base_register, index_register, scale) and preface it with the offset.

example: movl    $0x6789cdef, -16(%edx, %eax, 4)

14.8 Exercises

14-1

(§14.1) Develop an algorithm for converting decimal fractions to binary. Hint: Multiply both sides of Equation 14.1 by two.

14-2

(§14.1) Show that two’s complement works correctly for fractional values. What is the decimal range of 8-bit, two’s complement fractional values? Hint: +0.5 does not exist, but -0.5 does.

14-3

(§14.3) Copy the following program and run it:

 
1/* 
2 * exer14_3.c 
3 * Use float for Loop Control Variable? 
4 * Bob Plantz - 18 June 2009 
5 */ 
6 
7#include <stdio.h> 
8 
9int main() 
10{ 
11    float number; 
12    int counter = 20; 
13 
14    number = 0.5; 
15    while ((number != 0.0) && (counter > 0)) 
16    { 
17        printf("number = %.10f and counter = %i\n", number, counter); 
18 
19        number -= 0.1; 
20        counter -= 1; 
21    } 
22 
23    return 0; 
24}
Listing 14.5: Use float for Loop Control Variable?

Explain the behavior. What happens if you change the decrement of number from 0.1 to 0.0625? Explain.

14-4

(§14.3 §14.4) Copy the following program and run it:

 
1/* 
2 * exer14_3.c 
3 * Are floats accurate? 
4 * Bob Plantz - 18 June 2009 
5 */ 
6 
7#include <stdio.h> 
8 
9int main() 
10{ 
11    float fNumber = 2147483646.0; 
12    int iNumber = 2147483646; 
13 
14    printf(" Before adding the float is %f\n", fNumber); 
15    printf("         and the integer is %i\n\n", iNumber); 
16    fNumber += 1.0; 
17    iNumber += 1; 
18    printf("After adding 1 the float is %f\n", fNumber); 
19    printf("         and the integer is %i\n", iNumber); 
20 
21    return 0; 
22}
Listing 14.6: Are floats accurate?

Explain the behavior. What is the maximum value of fNumber such that adding 1.0 to it works?

14-5

(§14.4) Convert the following decimal numbers to 32-bit IEEE 754 format by hand:

a) 1.0 b) -0.1 c) 2005.0 d) 0.00390625 e) -3125.3125 f) 0.33 g) -0.67 h) 3.14

14-6

(§14.4) Convert the following 32-bit IEEE 754 bit patterns to decimal.

a) 4000 0000 b) bf80 0000 c) 3d80 0000 d) c180 4000 e) 42c8 1000 f) 3f99 999a g) 42f6 e666 h) c259 48b4

14-7

(§14.4) Show that half the floats (in 32-bit IEEE 754 format) are between -2.0 and +2.0.

14-8

(§14.5) The following C program

 
1/* 
2 * casting.c 
3 * Casts two integers to floats and adds them. 
4 * Bob Plantz - 18 June 2009 
5 */ 
6 
7#include <stdio.h> 
8 
9int main() 
10{ 
11    int x; 
12    double y, z; 
13 
14    printf("Enter an integer: "); 
15    scanf("%i", &x); 
16    y = 1.23; 
17    z = (double)x + y; 
18    printf("%i + %lf = %lf\n", x, y, z); 
19 
20    return 0; 
21}
Listing 14.7: Casting integer to float in C.

was compiled with the -S option to produce

 
1        .file  "casting.c" 
2        .section      .rodata 
3.LC0: 
4        .string"Enter an integer: " 
5.LC1: 
6        .string"%i" 
7.LC3: 
8        .string"%i + %lf = %lf\n" 
9        .text 
10        .globlmain 
11        .type  main, @function 
12main: 
13        pushq  %rbp 
14        movq  %rsp, %rbp 
15        subq  $48, %rsp 
16        movl  $.LC0, %edi 
17        movl  $0, %eax 
18        call  printf 
19        leaq  -20(%rbp), %rax 
20        movq  %rax, %rsi 
21        movl  $.LC1, %edi 
22        movl  $0, %eax 
23        call  __isoc99_scanf 
24        movabsq$4608218246714312622, %rax 
25        movq  %rax, -16(%rbp) 
26        movl  -20(%rbp), %eax 
27        cvtsi2sd      %eax, %xmm0 
28        addsd  -16(%rbp), %xmm0 
29        movsd  %xmm0, -8(%rbp) 
30        movl  -20(%rbp), %ecx 
31        movq  -8(%rbp), %rdx 
32        movq  -16(%rbp), %rax 
33        movq  %rdx, -40(%rbp) 
34        movsd  -40(%rbp), %xmm1 
35        movq  %rax, -40(%rbp) 
36        movsd  -40(%rbp), %xmm0 
37        movl  %ecx, %esi 
38        movl  $.LC3, %edi 
39        movl  $2, %eax 
40        call  printf 
41        movl  $0, %eax 
42        leave 
43        ret 
44        .size  main, .-main 
45        .ident"GCC: (Ubuntu/Linaro 4.7.0-7ubuntu3) 4.7.0" 
46        .section      .note.GNU-stack,"",@progbits
Listing 14.8: Casting integer to float in assembly language.

Identify the assembly language sequence that performs the C sequence

15   y = 1.23; 
16   z = (double)x + y;

and describe what occurs.

[next] [prev] [prev-tail] [front] [up]