2: for i = 0 to N do
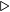 i-th bit
i-th bit 3: sumi ← (xi + yi + carry) % 10
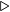 mod operation
mod operation 4: carry ← (xi + yi + carry) ∕ 10
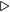 div operation
div operation 5: end for
We next turn our attention to a code for storing decimal integers. Since all storage in a computer is by means of on/off switches, we cannot simply store integers as decimal digits. Exercises 3-1 and 3-2 should convince you that it will take some thought to come up with a good code that uses simple on/off switches to represent decimal numbers.
Another very important issue when talking about computer arithmetic was pointed out in Section 2.3 (page 28). Namely, the programmer must decide how many bits will be used for storing the numbers before performing any arithmetic operations. This raises the possibility that some results will not fit into the allocated number of bits. As you will see in Section 9.2 (page 607), the computer hardware provides for this possibility with the Carry Flag (CF) and Overflow Flag (OF) in the rflags register located in the CPU. Depending on what you intend the bit patterns to represent, either the Carry Flag or the Overflow Flag (not both) will indicate the correctness of the result. However, most high level languages, including C and C++, do not check the CF and OF after performing arithmetic operations.
Computers perform addition in the binary number system.1 The operation is really quite easy to understand if you recall all the details of performing addition in the decimal number system by hand. Since most people perform addition on a calculator these days, let us review all the steps required when doing it by hand. Consider two two-digit numbers, x = 67 and y = 79. Adding these by hand on paper would look something like:
| 1 | 1 | ←− carries | ||
| 67 | ←− x | |||
| + | 79 | ←− y | ||
| 46 | ←− sum |
We start by working from the right, adding the two decimal digits in the ones place. 7 + 9 exceeds 10 by 6. We show this by placing a 6 in the ones place in the sum and carrying a 1 to the tens place. Next we add the three decimal digits in the tens place, 1 (the carry into the tens place from the ones place) + 6 + 7. The sum of these three digits exceeds 10 by 4, which we show by placing a 4 in the tens place in the sum and recording the fact that there is an ultimate carry of one. Recall that we had decided to use only two digits, so there is no hundreds place. Using the notation of Equation 2.5 (page 24), we describe addition of two decimal integers in Algorithm 3.1.
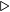 i-th bit
i-th bit 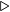 mod operation
mod operation 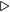 div operation
div operation Notice that:
By changing “10” to “2" we get Algorithm 3.2 for addition in the binary number system. The only difference is that a digit one place to the left counts two times more.
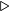 i-th bit
i-th bit 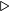 mod operation
mod operation 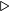 div operation
div operation Example 3-a ______________________________________________________________________________________________________
Compute the sum of x = 10101011 and y = 11001101.
Solution:
| 0 | 0001 | 111 | ←− carries | |
| 1010 | 1011 | ←− x | ||
| + | 0100 | 1101 | ←− y | |
| 1111 | 1000 | ←− sum |
This is how the algorithm was applied.
| one | s place: |
| sum0 = (1 + 1) % 2 = 0 |
| carry = (1 + 1) / 2 = 1 |
| twos place: |
| sum1 = (1 + 1 + 0) % 2 = 0 |
| carry = (1 + 1 + 0) / 2 = 1 |
| fours place: |
| sum2 = (1 + 0 + 1) % 2 = 0 |
| carry = (1 + 0 + 1) / 2 = 1 |
| eights place: |
| sum3 = (1 + 1 + 1) % 2 = 1 |
| carry = (1 + 1 + 1) / 2 = 1 |
| sixteens place: |
| sum4 = (1 + 0 + 0) % 2 = 1 |
| carry = (1 + 0 + 0) / 2 = 0 |
| thirty-twos place: |
| sum5 = (0 + 1 + 0) % 2 = 1 |
| carry = (0 + 1 + 0) / 2 = 0 |
| sixty-fours place: |
| sum6 = (0 + 0 + 0) % 2 = 1 |
| carry = (0 + 0 + 0) / 2 = 0 |
| one hundred twenty-eights place: |
| sum7 = (0 + 1 + 0) % 2 = 1 |
| carry = (0 + 1 + 0) / 2 = 0 |
In this eight-bit example the result is 1111 1000, and there is no carry beyond the eight bits. The lack of carry is recorded in the rflags register by setting the CF bit to zero.
__________________________________________________________________________________□
It should not surprise you that this algorithm also works for hexadecimal. In fact, it works for any radix, as shown in Algorithm 3.3.
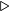 i-th digit
i-th digit 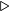 mod operation
mod operation 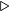 div operation
div operation For hexadecimal:
Addition in hexadecimal brings up a notational issue. For example,
Although it is certainly possible to perform all the computations using hexadecimal notation, most people find it a little awkward. After you have memorized Table 3.1 it is much easier to :
Actually, we did this when applying the algorithm to binary addition. Since the conversion of binary digits to decimal digits is trivial, you probably did not think about it. But the conversion of hexadecimal digits to decimal is not as trivial. To see how it works, first recall that the conversion from hexadecimal to binary is straightforward. (You should have memorized Table 2.1 by now.) So we will consider conversion from binary to decimal.
As mentioned above, the relative position of each bit has significance. The rightmost bit represents the ones place, the next one to the left the fours place, then the eights place, etc. In other words, each bit represents 2n, where n = 0, 1, 2, 3,... and we start from the right. So the binary number 1011 represents:
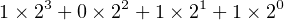 | (3.1) |
This is easily converted to decimal by simply working out the arithmetic in decimal:
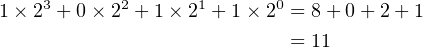 | (3.2) |
From Table 2.1 on page 18 we see that 10112 = b16, and we conclude that b16 = 1110. We can add a “decimal” column to the table, giving Table 3.1.
| Four binary digits (bits) | One hexadecimal digit | Decimal equivalent |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | a | 10 |
| 1011 | b | 11 |
| 1100 | c | 12 |
| 1101 | d | 13 |
| 1110 | e | 14 |
| 1111 | f | 15 |
Example 3-b ______________________________________________________________________________________________________
Compute the sum of x = 0xabcd and y = 0x6089.
Solution:
| 1 | 011 | ←− carries | |
| abcd | ←− x | ||
| + | 6089 | ←− y | |
| 0c56 | ←− sum |
Now we can see how Algorithm 3.3 with radix = 16 was applied in order to add the hexadecimal numbers, abcd and 6089. Having memorized Table 3.1, we will convert between hexadecimal and decimal “in our heads.”
| one | s place: |
| sum0 = (d + 9) % 16 = 6 |
| carry = (d + 9) / 16 = 1 |
| sixteens place: |
| sum1 = (1 + c + 8) % 16 = 5 |
| carry = (1 + c + 8) / 16 = 1 |
| two hundred fifty-sixes place: |
| sum2 = (1 + b + 0) % 16 = c |
| carry = (1 + b + 0) / 16 = 0 |
| four thousand ninety-sixes place: |
| sum3 = (0 + a + 6) % 16 = 0 |
| carry = (0 + a + 6) / 16 = 1 |
This four-digit example has an ultimate carry of 1, which is recorded in the rflags register by setting the CF to one. The arithmetic was performed by first converting each digit to decimal. It is then a simple matter to convert each decimal value back to hexadecimal (see Table 3.1) to express the final answer in hexadecimal.
__________________________________________________________________________________□
Let us now turn to the subtraction operation. As you recall from subtraction in the decimal number system, you must sometimes borrow from the next higher-order digit in the minuend. This is shown in Algorithm 3.4.
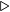 i-th digit
i-th digit 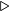 subtract Y from X
subtract Y from X 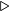 Result will be wrong!
Result will be wrong! This algorithm is not as complicated as it first looks.
Example 3-c ______________________________________________________________________________________________________
Subtract y = 10101011 from x = 11001101.
Solution:
| 0 | 0100 | 010 | ←− borrows | |
| 1100 | 1101 | ←− x | ||
| - | 1010 | 1011 | ←− y | |
| 0010 | 0010 | ←− difference |
The bits have been grouped to improve readability. Each number (0 or 1) in the borrows row shows the
intermediate borrow that came from the minuend in that place, which becomes 2 in the next place to the
right. A 1 indicates that borrow was required from this bit position, a 0 indicates no borrow. This is how the
algorithm was applied.
| one | s place: |
| difference0 = 1 - 1 = 0 |
| twos place: |
| Borrow from the fours place in the minuend. |
| The borrow becomes 2 in the twos place. |
| difference1 2 - 1 = 1 |
| fours place: |
| Since we borrowed 1 from here, the minuend has a 0 left. |
| difference2 = 0 - 0 = 0 |
| eights place: |
| difference3 = 1 - 1 = 0 |
| sixteens place: |
| difference4 = 0 - 0 = 0 |
| thirty-twos place: |
| Borrow from the sixty-fours place in the minuend. |
| The borrow becomes 2 in the thirty-twos place. |
| difference5 = 2 - 1 = 1 |
| sixty-fours place: |
| Since we borrowed 1 from here, the minuend has a 0 left. |
| difference6 = 0 - 0 = 0 |
| one hundred twenty-eights place: |
| difference7 = 1 - 1 = 0 |
_______________________________________________________________________________□
This, of course, also works for hexadecimal, but remember that a digit one place to the left counts sixteen times more. For example, consider x = 0x6089 and y = 0xab5d:
| 1 | 101 | ←− borrows | ||
| 6089 | ←− x | |||
| - | ab5d | ←− y | ||
| b52c | ←− sum |
Notice in this second example that we had to borrow from “beyond the width” of the two values. That is, the two values are each sixteen bits wide, and the result must also be sixteen bits. Whether there is borrow “from outside” to the high-order digit is recorded in the CF of the rflags register whenever a subtract operation is performed:
Another way to state this is for unsigned numbers:
The binary number system was introduced in Section 2.2 (page 23). You undoubtedly realize by now that it probably is a good system for storing unsigned integers. Don’t forget that it does not matter whether we think of the integers as being in decimal, hexadecimal, or binary since they are mathematically equivalent. If we are going to store integers this way, we need to consider the arithmetic properties of addition and subtraction in the binary number system. Since a computer performs arithmetic in binary (see footnote 1 on page 66), we might ask whether addition yields arithmetically correct results when representing decimal numbers in the binary number system. We will use four-bit values to simplify the discussion. Consider addition of the two numbers:
| 01002 | = | 0 ×23+ 1 ×22+ 0 ×21+ 0 ×20 | = | 4 10 |
| + 00102 | = | 0 ×23+ 0 ×22+ 1 ×21+ 0 ×20 | = | + 2 10 |
| 01102 | = | 0 ×23+ 1 ×22+ 1 ×21+ 0 ×20 | = | 6 10 |
and CF = 0.
So far, the binary number system looks reasonable. Let’s try two larger four-bit numbers:
| 01002 | = | 0 ×23+ 1 ×22+ 0 ×21+ 0 ×20 | = | 4 10 |
| + 11102 | = | 1 ×23+ 1 ×22+ 1 ×21+ 0 ×20 | = | +14 10 |
| 00102 | = | 0 ×23+ 0 ×22+ 1 ×21+ 0 ×20 | = | 2 10 |
and CF = 1. The result, 2, is arithmetically incorrect. The problem here is that the addition has produced carry beyond the fourth bit. Since this is not taken into account in the result, the answer is wrong.
Now consider subtraction of the two numbers:
| 01002 | = | 0 ×23+ 1 ×22+ 0 ×21+ 0 ×20 | = | 4 10 |
| - 11102 | = | 1 ×23+ 1 ×22+ 1 ×21+ 0 ×20 | = | -14 10 |
| 01102 | = | 0 ×23+ 1 ×22+ 1 ×21+ 0 ×20 | = | 6 10 |
and CF = 1.
The result, 6, is arithmetically incorrect. The problem in this case is that the subtraction has had to borrow from beyond the fourth bit. Since this is not taken into account in the result, the answer is wrong.
From the discussion in Section 3.1 (page 66) you should be able to convince yourself that these four-bit arithmetic examples generalize to any size arithmetic performed by the computer. After adding two numbers, the Carry Flag will always be set to zero if there is no ultimate carry, or it will be set to one if there is ultimate carry. Subtraction will set the Carry Flag to zero if no borrow from the “outside” is required, or one if borrow is required. These examples illustrate the principle:
It is important to realize that the CF and OF bits in the rflags register are always set to the appropriate value, 0 or 1, each time an addition or subtraction is performed by the CPU. In particular, the CPU will not ignore the CF when there is no carry, it will actively set the CF to zero.
When representing signed decimal integers we have to use one bit for the sign. We might be tempted to simply use the highest-order bit for this purpose. Let us say that 0 means + and 1 means -. We will try adding (+2) and (-2):
| 00102 | = | (+2)10 |
| + 10102 | = | + (-2)10 |
| 11002 | = | (-4)10 |
The result, -4, is arithmetically incorrect. We should note here that the problem is the way in which the computer does addition — it performs binary addition on the bit patterns that in themselves have no inherent meaning. There are computers that use this particular code for storing signed decimal integers. They have a special “signed add” instruction. By the way, notice that such computers have both a +0 and a -0!
Most computers, including the x86, use another code for representing signed decimal integers — the two’s complement code. To see how this code works, we start with an example using the decimal number system.
Say that you have a cassette player and wish to represent both positive and negative positions on the tape. It would make sense to somehow fast-forward the tape to its center and call that point “zero.” Most cassette players have a four decimal digit counter that represents tape position. The counter, of course, does not give actual tape position, but a “coded” representation of the tape position. Since we wish to call the center of the tape “zero,” we push the counter reset button to set it to 0000.
Now, moving the tape forward — the positive direction — will cause the counter to increment. And moving the tape backward — the negative direction — will cause the counter to decrement. In particular, if we start at zero and move to “+1” the “code” on the tape counter will show 0001. On the other hand, if we start at zero and move to “-1” the “code” on the tape counter will show 9999.
Using our tape code system to perform the arithmetic in the previous example — (+2) + (-2):
The counter shows 0000, which is 0 according to our code.
Next we will perform the same arithmetic starting with (-2), then adding (+2):
The counter shows 0000, but there is a carry. (9998 + 2 = 0000 with carry = 1.) If we ignore the carry, the answer is correct. This example illustrates the principle:
The two’s complement code uses this pattern for representing signed decimal integers in bit patterns. The correspondence between signed decimal (two’s complement), hexadecimal, and binary for four-bit values is shown in Table 3.2.
| Four binary digits (bits) | One hexadecimal digit | Decimal equivalent |
| 1000 | 8 | -8 |
| 1001 | 9 | -7 |
| 1010 | a | -6 |
| 1011 | b | -5 |
| 1100 | c | -4 |
| 1101 | d | -3 |
| 1110 | e | -2 |
| 1111 | f | -1 |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
We make the following observations about Table 3.2:
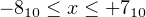 | (3.3) |
or
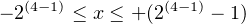 | (3.4) |
The last observation can be generalized for n bits to:
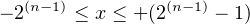 | (3.5) |
In the two’s complement code, the negative of any integer, x, is defined as
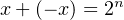 | (3.6) |
Notice that 2n written in binary is “1” followed by n zeros. That is, it requires n+1 bits to represent. Another way of saying this is, “in the n-bit two’s complement code adding a number to its negative produces n zeros and carry.”
We now derive a method for computing the negative of a number in the two’s complement code. Solving Equation 3.6 for −x, we get:
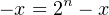 | (3.7) |
For example, if we wish to compute -1 in binary (in the two’s complement code) in 8 bits, we perform the arithmetic:
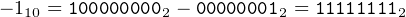 | (3.8) |
or in hexadecimal:
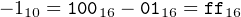 | (3.9) |
This subtraction is error prone, so let’s perform a few algebraic manipulations on Equation 3.7, which defines the negation operation. First, we subtract one from both sides:
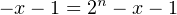 | (3.10) |
Rearranging a little:
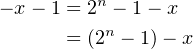 | (3.11) |
Now, consider the quantity (2n − 1). Since 2n is written in binary as one (1) followed by n zeros, (2n − 1) is written as n ones. For example, for n = 8:
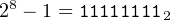 | (3.12) |
Thus, we can express the right-hand side of Equation 3.11 as
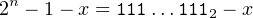 | (3.13) |
where 111…1112 designates n ones.
You can see how easy the subtraction on the right-hand side of Equation 3.13 is if we consider the previous example of computing -1 in binary in eight bits. Let x = 1, giving:
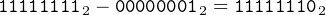 | (3.14) |
or in hexadecimal:
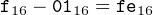 | (3.15) |
Another (simpler) way to look at this is
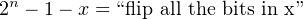 | (3.16) |
The value of the right-hand side of Equation 3.16 is called the reduced radix complement of x. Since the radix is two, it is common to call this the one’s complement of x. From Equation 3.11 we see that this computation — the reduced radix complement of x — gives
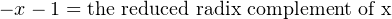 | (3.17) |
Now we can easily compute -x by adding one to both sides of Equation 3.17:
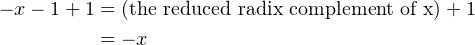 | (3.18) |
This leads us to Algorithm 3.5 for negating any integer stored in the two’s complement, n-bit code.
This process — computing the one’s complement, then adding one — is called computing the two’s complement.
Combining Algorithm 3.5 with observations about Table 3.2 above, we can easily compute the decimal equivalent of any integer stored in the two’s complement notation by applying Algorithm 3.6.
Example 3-d ______________________________________________________________________________________________________
The 16-bit integer 567816 is stored in two’s complement notation. Convert it to a signed, decimal integer.
Solution:
Since the high-order bit is zero, we simply compute the decimal equivalent:
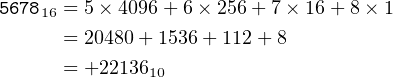 |
__________________________________________________________________________________□
Example 3-e ______________________________________________________________________________________________________
The 16-bit integer 876516 is stored in two’s complement notation. Convert it to a signed, decimal integer.
Solution:
Since the high-order bit is one, we first negate the number in the two’s complement format.
Take the one’s complement.
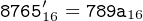 |
Add one.
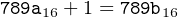 |
Place a minus sign in front of the number (since we negated it in the two’s complement domain).
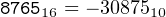 |
__________________________________________________________________________________□
Algorithm 3.7 shows how to convert a signed decimal number to two’s complement binary.
Example 3-f ______________________________________________________________________________________________________
Convert the signed, decimal integer +31693 to a 16-bit integer in two’s complement notation. Give the answer in hexadecimal.
Solution:
Since this is a positive number, we simply convert it. The answer is to be given in hexadecimal, so we will repetitively divide by 16 to get the answer.
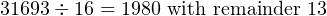 |
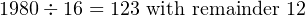 |
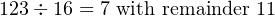 |
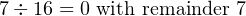 |
So the answer is
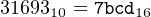 |
__________________________________________________________________________________□
Example 3-g ______________________________________________________________________________________________________
Convert the signed, decimal integer -250 to a 16-bit integer in two’s complement notation. Give the answer in hexadecimal.
Solution:
Since this is a negative number, we first negate it, giving +250. Then we convert this value. The answer is to be given in hexadecimal, so we will repetitively divide by 16 to get the answer.
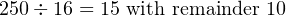 |
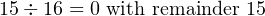 |
This gives us
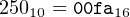 |
Now we take the one’s complement:
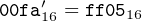 |
And add one:
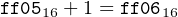 |
So the answer is:
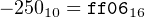 |
__________________________________________________________________________________□
The number of bits used to represent a value is determined at the time a program is written. So when performing arithmetic operations we cannot simply add more digits (bits) if the result is too large, as we can do on paper. You saw in Section 3.1 (page 66) that the CF indicates when the sum of two unsigned integers exceeds the number of bits allocated to it.
In Section 3.3 (page 87) you saw that carry is irrelevant when working with signed integers. You also saw that adding two signed numbers can produce an incorrect result. That is, the sum may exceed the range of values that can be represented in the allocated number of bits.
The flags register, rflags, provides a bit, the Overflow Flag (OF), for detecting whether the sum of two n-bit, signed numbers stored in the two’s complement code has exceeded the range allocated for it. Each operation that affects the overflow flag sets the bit equal to the exclusive or of the carry into the highest-order bit of the operands and the ultimate carry. For example, when adding the two 8-bit numbers, 1516 and 6f16, we get:
| carry −→ | 0 | 1 ←− penultimate carry
| |||
| 0001 | 0101 | ←− x | |||
| + | 0110 | 1111 | ←− y | ||
| 1000 | 0100 | ←− sum | |||
In this example, there is a carry of zero and a penultimate (next to last) carry of one. The OF flag is equal to the exclusive or of carry and penultimate carry:
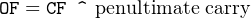 | (3.19) |
where ‘^’ is the exclusive or operator. In the above example
| OF | = 0 ^ 1 | ||
| = 1 | (3.20) |
There are three cases when adding two numbers:
| x | = 1… | ||
| y | = 0… |
That is, the high-order bit of one number is 1 and the high-order bit of the other is 0, regardless of what the other bits are. Now, if we add x and y, there are two possible results with respect to carry:
| carry −→ 0 | 0 | ←− penultimate carry
| |
| 0 | … | ←− x | |
| + | 1 | … | ←− y |
| 1 | … | ←− sum | |
this addition would produce OF = 0 ^ 0 = 0.
| carry −→ 1 | 1 | ←− penultimate carry
| |
| 0 | … | ←− x | |
| + | 1 | … | ←− y |
| 0 | … | ←− sum | |
this addition would produce OF = 1 ^ 1 = 0.
We conclude that adding two integers of opposite sign always yields 0 for the overflow flag.
Next, notice that since y is positive and x negative:
| 0 | ≤ y ≤ +(2(n−1) − 1) | (3.21) |
| − 2(n−1) | ≤ x < 0 | (3.22) |
Adding inequalities (3.21) and (3.22), we get:
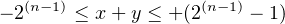 | (3.23) |
Thus, the sum of two integers of opposite sign remains within the range of signed integers, and there is no overflow (OF = 0).
| x | = 0… | ||
| y | = 0… |
That is, the high-order bit is 0, regardless of what the other bits are. Now, if we add x and y, there are two possible results with respect to carry:
| carry −→ 0 | 0 | ←− penultimate carry
| |
| 0 | … | ←− x | |
| + | 0 | … | ←− y |
| 0 | … | ←− sum | |
this addition would produce OF = 0 ^ 0 = 0. The high-order bit of the sum is zero, so it is a positive number, and the sum is within range.
| carry −→ 0 | 1 | ←− penultimate carry
| |
| 0 | … | ←− x | |
| + | 0 | … | ←− y |
| 1 | … | ←− sum | |
this addition would produce OF = 0 ^ 1 = 1. The high-order bit of the sum is one, so it is a negative number. Adding two positive numbers cannot yield a negative sum, so this sum has exceeded the allocated range.
| x | = 1… | ||
| y | = 1… |
That is, the high-order bit is 1, regardless of what the other bits are. Now, if we add x and y, there are two possible results with respect to carry:
| carry −→ 1 | 0 | ←− penultimate carry
| |
| 1 | … | ←− x | |
| + | 1 | … | ←− y |
| 0 | … | ←− sum | |
this addition would produce OF = 1 ^ 0 = 1. The high-order bit of the sum is zero, so it is a positive number. Adding two negative numbers cannot yield a negative sum, so this sum has exceeded the allocated range.
| carry −→ 1 | 1 | ←− penultimate carry
| |
| 1 | … | ←− x | |
| + | 1 | … | ←− y |
| 1 | … | ←− sum | |
this addition would produce OF = 1 ^ 1 = 0. The high-order bit of the sum is one, so it is a negative number, and the sum is within range.
These results, together with the results from Section 3.2 (page 86), yield the following rules when adding or subtraction two n-bit integers:
The CPU does not consider integers as either signed or unsigned. Both the CF and OF are set according to the rules of binary arithmetic by each arithmetic operation. The distinction between signed and unsigned is completely determined by the program. After each addition or subtraction operation the program should check the state of the CF for unsigned integers or the OF of signed integers and at least indicate when the sum is in error. Most high-level languages do not perform this check, which can lead to some obscure program bugs.
The codes used for both unsigned integers and signed integers are circular in nature. That is, for a given number of bits, each code “wraps around.” This can be seen pictorially in the “Decoder Ring” shown in Figure 3.1 for three-bit numbers.
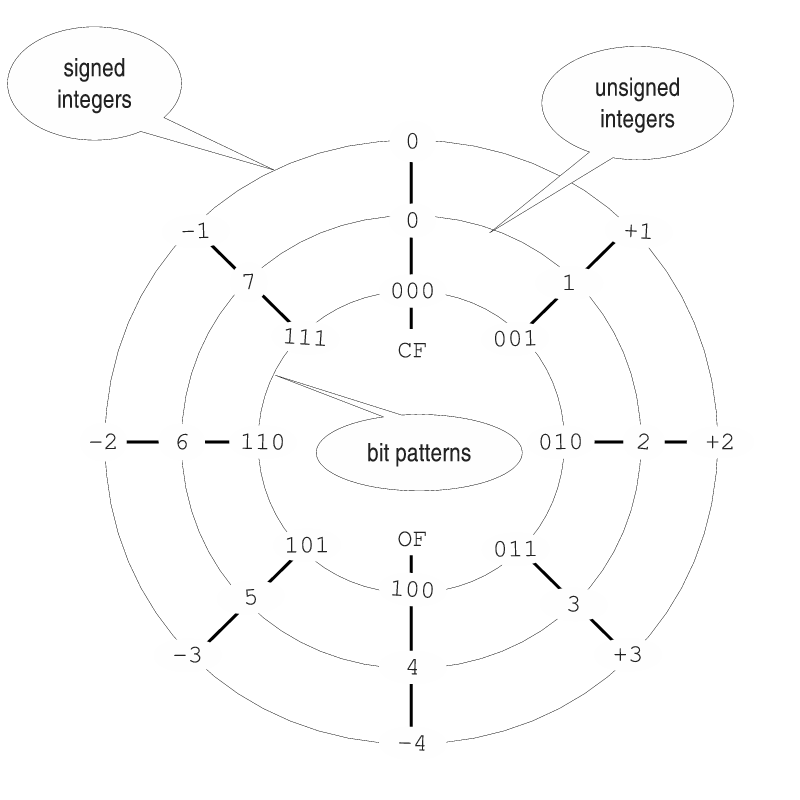
Example 3-h ______________________________________________________________________________________________________
Using the “Decoder Ring” (Figure 3.1), add the unsigned integers 3 + 4.
Solution:
Working only in the inner ring, start at the tic mark for 3, which corresponds to the bit pattern 011. The bit pattern corresponding to 4 is 100, which is four tic marks CW from zero. So move four tic marks CW from the 3 tic mark. This places us at the tic mark labeled 111, which corresponds to 7. Since we did not reach the tic mark at the top of the Decoder Ring, CF = 0. Thus, the result is correct.
__________________________________________________________________________________□
Example 3-i _______________________________________________________________________________________________________
Using the “Decoder Ring” (Figure 3.1), add the unsigned integers 5 + 6.
Solution:
Working only in the inner ring, start at the tic mark for 5, which corresponds to the bit pattern 101. The bit pattern corresponding to 6 is 110, which is six tic marks CW from zero. So move six tic marks CW from the 5 tic mark. This places us at the tic mark labeled 011, which corresponds to 3. Since we have reached the tic mark at the top of the Decoder Ring, CF = 1. Thus, the result is incorrect.
__________________________________________________________________________________□
Example 3-j _______________________________________________________________________________________________________
Using the “Decoder Ring” (Figure 3.1), add the signed integers (+1) + (+2).
Solution:
Working only in the outer ring, start at the tic mark for +1, which corresponds to the bit pattern 001. The bit pattern corresponding to +2 is 010, which is two tic marks CW from zero. So move two tic marks CW from the +1 tic mark. This places us at the tic mark labeled 011, which corresponds to +3. Since we did not reach the tic mark at the bottom of the Decoder Ring, OF = 0. Thus, the result is correct.
__________________________________________________________________________________□
Example 3-k ______________________________________________________________________________________________________
Using the “Decoder Ring” (Figure 3.1), add the signed integers (+3) + (-4).
Solution:
Working only in the outer ring, start at the tic mark for +3, which corresponds to the bit pattern 011. The bit pattern corresponding to -4 is 100, which is four tic marks CCW from zero. So move four tic marks CCW from the +3 tic mark. This places us at the tic mark labeled 111, which corresponds to -1. Since we did not reach the tic mark at the bottom of the Decoder Ring, OF = 0. Thus, the result is correct.
__________________________________________________________________________________□
Example 3-l _______________________________________________________________________________________________________
Using the “Decoder Ring” (Figure 3.1), add the signed integers (+3) + (+1).
Solution:
Working only in the outer ring, start at the tic mark for +3, which corresponds to the bit pattern 011. The bit pattern corresponding to +1 is 001, which is one tic mark CW from zero. So move one tic mark CW from the +3 tic mark. This places us at the tic mark labeled 100, which corresponds to -4. Since we reached the tic mark at the bottom of the Decoder Ring, OF = 1. Thus, the result is incorrect.
__________________________________________________________________________________□
High-level languages provide some basic data types. For example, C/C++ provides int, char, float, etc. The sizes of some data types are shown in Table 3.3.
| Data type | 32-bit mode | 64-bit mode |
| char | 8 | 8 |
| int | 32 | 32 |
| long | 32 | 64 |
| long long | 64 | 64 |
| float | 32 | 32 |
| double | 64 | 64 |
| *any | 32 | 64 |
The sizes given in this table are taken from the System V Application Binary Interface specifications, reference [33] for 32-bit and reference [25] for 64-bit, and are used by the gcc compiler for the x86-64 architecture. Language specifications tend to be more permissive in order to accommodate other hardware architectures. For example, see reference [10] for the specifications for C.
A given “real world” value can usually be represented in more than one data type. For example, most people would think of “123” as representing “one hundred twenty-three.” This value could be stored in a computer in int format or as a text string. An int in our C/C++ environment is stored in 32 bits, and the bit pattern would be
As a C-style text string, it would also require four bytes of memory, but their bit patterns would be
The int format is easier to use in arithmetic and logical expressions, but the interface with the outside world through the screen and the keyboard uses the char format. If a user entered 123 from the keyboard, the operating system would read the individual characters, each in char format. The text string must be converted to int format. After the numbers are manipulated, the result must be converted from the int format to char format for display on the screen.
C programmers use functions in the stdio library and C++ programmers use functions in the iostream library to do these conversions between the int and char formats. For example, the C code sequence
or the C++ code sequence
The C or C++ I/O library functions in the code segments above do the necessary conversions between character sequences and the int storage format. However, once the conversion is performed, they ultimately call the read system call function to read bytes from the keyboard and the write system call function to write bytes to the screen. As shown in Figure 3.2, an application program can call the read and write functions directly to transfer bytes.
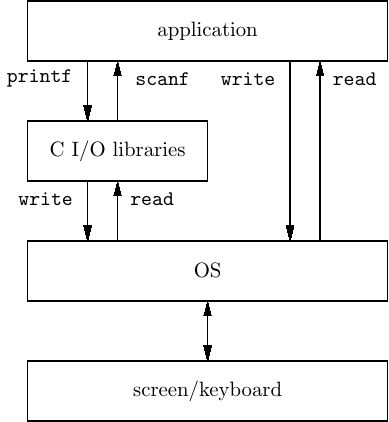
When using the read and write system call functions for I/O, it is the programmer’s responsibility to do the conversions between the char type used for I/O and the storage formats used within the program. We will soon be writing our own functions in assembly language to convert between the character format used for screen display and keyboard input, and the internal storage format of integers in the binary number system. The purpose of writing our own functions is to gain a thorough understanding of how data is represented internally in the computer.
Since our primary goal here is to study storage formats, we will concentrate on bit patterns. We will develop a program in C that allows a user to enter bit patterns in hexadecimal. The program will read the characters from the keyboard in ASCII code and convert them into the corresponding int storage format as shown in Algorithm 3.8. This conversion algorithm involves manipulating data at the bit level.
Let us examine this algorithm. Each character read from the keyboard represents a hexadecimal digit. That is, each character is one of ‘0’, …,‘9’,‘a’, …,‘f’. (We assume that the user does not make mistakes.) Since a hexadecimal digit represents four bits, we need to shift the accumulated integer four bits to the left in order to make room for the new four-bit value.
You should recognize that shifting an integer four bits to the left multiplies it by 16. As you will see in Sections 12.3 and 12.4 (pages 760 and 777), multiplication and division are complicated operations, and they can take a great deal of processor time. Using left/right shifts to effect multiplication/division by powers of two is very efficient. More importantly, the four-bit shift is more natural in this application.
The C/C++ operator for shifting bits to the left is «.2 For example, if x is an int, the statement
shifts the value in x four bits to the left, thus multiplying it by sixteen. Similarly, the C/C++ operator for shifting bits to the right is ». For example, if x is an int, the statement
shifts the value in x three bits to the right, thus dividing it by eight. Note that the three right-most bits are lost, so this is an integer div operation. The program in Listing 3.1 illustrates the use of the C shift operators to multiply and divide by powers of two.
We begin by reviewing the C/C++ bitwise logical operators,
| and | & |
| or | | |
| exclusive or | ^ |
| complement | ∼ |
It is easy to see what each of these operators does by using truth tables. To illustrate how truth tables work, consider the algorithm for binary addition. In Section 3.1 (page 66) we saw that the ith bit in the result is the sum of the ith bit of one number plus the ith bit of the other number plus the carry produced from adding the (i-1)th bits. This sum will produce a carry of zero or one. In other words, a bit adder has three inputs — the two corresponding bits from the two numbers being added and the carry from the previous bit addition — and two outputs — the result and the carry. In a truth table we have a column for each input and each output. Then we write down all possible input bit combinations and then show the output(s) in the corresponding row. A truth table for the bit addition operation is shown in Figure 3.3. We use the notation x[i] to represent the ith bit in the variable x; x[i-j] would specify bits i through j.
| x[i] | y[i] | carry[(i-1)] | z[i] | carry[i] |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The bitwise logical operators act on the corresponding bits of two operands as shown in Figure 3.4.
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
Example 3-m _____________________________________________________________________________________________________
Let int x = 0x1234abcd. Compute the and, or, and xor with 0xdcba4321.
Solution:
__________________________________________________________________________________□
Make sure that you distinguish these bitwise logical operators from the C/C++ logical operators, &&, ||, and !. The logical operators work on groups of bits organized into integral data types rather than individual bits. For comparison, the truth tables for the C/C++ logical operators are shown in Figure 3.5
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
Now we are prepared to see how we can convert from the ASCII character code to the int format. The & operator works very nicely for the conversion. If a numeric character is stored in the char variable aChar, from Table 3.4 we see that the required operation is
| Hex character | ASCII code | Corresponding int |
| 0 | 0011 0000 | 0000 0000 0000 0000 0000 0000 0000 0000 |
| 1 | 0011 0001 | 0000 0000 0000 0000 0000 0000 0000 0001 |
| 2 | 0011 0010 | 0000 0000 0000 0000 0000 0000 0000 0010 |
| 3 | 0011 0011 | 0000 0000 0000 0000 0000 0000 0000 0011 |
| 4 | 0011 0100 | 0000 0000 0000 0000 0000 0000 0000 0100 |
| 5 | 0011 0101 | 0000 0000 0000 0000 0000 0000 0000 0101 |
| 6 | 0011 0110 | 0000 0000 0000 0000 0000 0000 0000 0110 |
| 7 | 0011 0111 | 0000 0000 0000 0000 0000 0000 0000 0111 |
| 8 | 0011 1000 | 0000 0000 0000 0000 0000 0000 0000 1000 |
| 9 | 0011 1001 | 0000 0000 0000 0000 0000 0000 0000 1001 |
| a | 0110 0001 | 0000 0000 0000 0000 0000 0000 0000 1010 |
| b | 0110 0010 | 0000 0000 0000 0000 0000 0000 0000 1011 |
| c | 0110 0011 | 0000 0000 0000 0000 0000 0000 0000 1100 |
| d | 0110 0100 | 0000 0000 0000 0000 0000 0000 0000 1101 |
| e | 0110 0101 | 0000 0000 0000 0000 0000 0000 0000 1110 |
| f | 0110 0110 | 0000 0000 0000 0000 0000 0000 0000 1111 |
Well, we still have an 8-bit value (with the four high-order bits zero), but we will work on this in a moment.
Next consider the alphabetic hexadecimal digits in Table 3.4. This table shows only the lower-case alphabetic characters, but you saw in Table 2.3 that the low-order four bits are the same for both upper- and lower-case alphbetic characters. We can use the same & operation to obtain these four bits, then add 9 to the result:
Conversion from the 8-bit char type to the 32-bit int type is accomplished by a type cast in C.
The resulting program is shown in Listing 3.2. Notice that we use the printf function to display the resulting stored value, both in hexadecimal and decimal. The conversion from stored int format to hexadecimal display is left as an exercise (Exercise 3-13).
Thus far in this chapter we have used the binary number system to represent numerical values. It is an efficient code in the sense that each of the 2n bit patterns represents a value. On the other hand, there are some limitations in the code. We will explore some other codes in this section.
One limitation of using the binary number system is that a decimal number must be converted to binary before storing or performing arithmetic operations on it. And binary numbers must be converted to decimal for most real-world display purposes.
The Binary Coded Decimal (BCD) code is a code for individual decimal digits. Since there are ten decimal digits, the code must use four bits for each digit. The BCD code is shown in Table 3.5.
| Decimal digit | BCD code (four bits) |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
For example, in a 16-bit storage location the decimal number 1234 would be stored in the BCD code as
and in binary as
From Table 3.5 we can see that six bit patterns are “wasted.” The effect of this inefficiency is that a 16-bit storage location has a range of 0 – 9999 if we use BCD, but the range is 0 – 65535 if we use binary.
BCD is important in specialized systems that deal primarily with numerical data. There are I/O devices that deal directly with numbers in BCD without converting to/from a character code, for example, ASCII. The COBOL programming language supports a packed BCD format where two BCD characters are stored in each 8-bit byte. The last (4-bit) digit is used to store the sign of the number as shown in Table 3.6. The specific codes used depend upon the particular implementation.
| Sign | BCD code (four bits) |
| + | 1010 |
| - | 1011 |
| + | 1100 |
| - | 1101 |
| + | 1110 |
| unsigned | 1111 |
One of the problems with both the binary and BCD codes is that the difference between two adjacent values often requires that more than one bit be changed. For example, three bits must be changed when incrementing from 3 to 4 — 0011 to 0100. If the value is read during the time when the bits are being switched there may be an error. This is more apt to occur if the bits are implemented with, say, mechanical switches instead of electronic. The Gray code is one where there is only one bit that differs between any two adjacent values. As you will see in Section 4.3, this property also allows for a very useful visual tool for simplifying Boolean algebra expressions.
The Gray code is easily constructed. Start with one bit:
| decimal | Gray code |
| 0 | 0 |
| 1 | 1 |
To add a bit, first duplicate the existing pattern, but reflected:
| Gray code | |
| 0 | |
| 1 | |
| 1 | |
| 0 | |
then add a zero to the beginning of each of the original bit patterns and a 1 to each of the reflected ones:
| decimal | Gray code |
| 0 | 00 |
| 1 | 01 |
| 2 | 11 |
| 3 | 10 |
Let us repeat these two steps to add another bit. Reflect the pattern:
| Gray code | |
| 00 | |
| 01 | |
| 11 | |
| 10 | |
| 10 | |
| 11 | |
| 01 | |
| 00 | |
then add a zero to the beginning of each of the original bit patterns and a 1 to each of the reflected ones:
| decimal | Gray code |
| 0 | 000 |
| 1 | 001 |
| 2 | 011 |
| 3 | 010 |
| 4 | 110 |
| 5 | 111 |
| 6 | 101 |
| 7 | 100 |
The Gray code for four bits is shown in Table 3.7. Notice that the pattern of only changing one bit between adjacent values also holds when the bit pattern “wraps around.” That is, only one bit is changed when going from the highest value (15 for four bits) to the lowest (0).
| Decimal | Gray code |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0011 |
| 3 | 0010 |
| 4 | 0110 |
| 5 | 0111 |
| 6 | 0101 |
| 7 | 0100 |
| 8 | 1100 |
| 9 | 1101 |
| 10 | 1111 |
| 11 | 1110 |
| 12 | 1010 |
| 13 | 1011 |
| 14 | 1001 |
| 15 | 1000 |
(§3.1) How many bits are required to store a single decimal digit?
(§3.1) Using the answer from Exercise 1, invent a code for storing eight decimal digits in a thirty-two bit register. Using your new code, does binary addition produce the correct results?
(§3.3) Select several pairs of signed integers from Table 3.2, convert each to binary using the table, perform the binary addition, and check the results. Does this code always work?
(§3.3) If you did not select them in Exercise 3, add +4 and +5 using the four-bit, two’s complement code (from Table 3.2). What answer do you get?
(§3.3) If you did not select them in Exercise 3, add -4 and -5 using the four-bit, two’s complement code (from Table 3.2). What answer do you get?
(§3.3) Select any positive integer from Table 3.2. Add the binary representation for the positive value to the binary representation for the negative value. What is the four-bit result? What is the value of the CF? The OF? If you do the addition “on paper” (that is, you can use as many digits as you wish), how could you express, in English, the result of adding the positive representation of an integer to its negative representation in the two’s complement notation? The negative representation to the positive representation? Which two integers do not have a representation of the opposite sign?
(§3.3) The following 8-bit hexadecimal values are stored in two’s complement format. What are the equivalent signed decimal numbers?
a) 55 b) aa c) f0 d) 0f e) 80 f) 63 g) 7b
(§3.3) The following 16-bit hexadecimal values are stored in two’s complement format. What are the equivalent signed decimal numbers?
a) 1234 b) edcc c) fedc d) 07d0 e) 8000 f) 0400 g) ffff h) 782f
(§3.3) Show how each of the following signed, decimal integers would be stored in 8-bit two’s complement format. Give your answer in hexadecimal.
a) 100 b) -1 c) -10 d) 88 e) 127 f) -16 g) -32 h) -128
(§3.3) Show how each of the following signed, decimal integers would be stored in 16-bit two’s complement format. Give your answer in hexadecimal.
a) 1024 b) -1024 c) -1 d) 32767 e) -256 f) -32768 g) -32767 h) -128
(§3.4) Perform binary addition of the following pairs of 8-bit numbers (shown in hexadecimal) and indicate whether your result is “right” or “wrong.” First treat them as unsigned values, then as signed values (stored in two’s complement format). Thus, you will have two “right/wrong” answers for each sum. Note that the computer performs only one addition, setting both the CF and OF according to the results of the addition. It is up to the program to test the appropriate flag depending on whether the numbers are being considered as unsigned or signed in the program.
a) 55 + aa b) 55 + f0 c) 80 + 7b d) 63 + 7b e) 0f + ff f) 80 + 80
(§3.4, 3.5) Perform binary addition of the following pairs of 16-bit numbers (shown in hexadecimal) and indicate whether your result is “right” or “wrong.” First treat them as unsigned values, then as signed values (stored in two’s complement format). Thus, you will have two “right/wrong” answers for each sum. Note that the computer performs only one addition, setting both the CF and OF according to the results of the addition. It is up to the program to test the appropriate flag depending on whether the numbers are being considered as unsigned or signed in the program.
a) 1234 + edcc b) 1234 + fedc c) 8000 + 8000 d) 0400 + ffff e) 07d0 + 782f f) 8000 + ffff
(§3.5) Enter the program in Listing 3.1 and get it to work. Use the program to compute 1 (one) multiplied by 2 raised to the 31st power. What result do you get for 1 (one) multiplied by 2 raised to the 32nd power? Explain the results.
(§3.5) Write a C program that prompts the user to enter a hexadecimal value, multiplies it by ten, then displays the result in hexadecimal. Your main function should
declare a char array,
call the readLn function to read from the keyboard,
call a function to convert the input text string to an int,
multiply the int by ten,
call a function to convert the int to its corresponding hexadecimal text string,
call writeStr to display the resulting hexadecimal text string.
Use the readLn and writeStr functions from Exercise 2 -32 to read from the keyboard and display on the screen. Place the functions to perform the conversions in separate files. Hint: review Figure 3.2.
(§3.5) Write a C program that prompts the user to enter a binary value, multiplies it by ten, then displays the result in binary. (“Binary” here means that the user communicates with the program in ones and zeros.) Your main function should
declare a char array,
call the readLn function to read from the keyboard,
call a function to convert the input text string to an int,
multiply the int by ten,
call a function to convert the int to its corresponding binary text string,
call writeStr to display the resulting binary text string.
Use the readLn and writeStr functions from Exercise 2 -32 to read from the keyboard and display on the screen. Your functions to convert from a binary text string to an int and back should be placed in separate functions.
(§3.5) Write a C program that prompts the user to enter unsigned decimal integer, multiplies it by ten, then displays the result in binary. (“Binary” here means that the user communicates with the program in ones and zeros.) Your main function should
declare a char array,
call the readLn function to read from the keyboard,
call a function to convert the input text string to an int,
multiply the int by ten,
call a function to convert the int to its corresponding decimal text string,
call writeStr to display the resulting decimal text string.
Use the readLn and writeStr functions from Exercise 2 -32 to read from the keyboard and display on the screen. Your function to convert from a decimal text string to an int should be placed in a separate function. Hint: this problem cannot be solved by simply shifting bit patterns. Think carefully about the mathematical equivalence of shifting bit patterns left or right.
(§3.5) Modify the program in Exercise 3-16 so that it works with signed decimal integers.