5 Logic Circuits

Chapter 5
Logic Circuits

In this chapter we examine how the concepts in Chapter 4 can be used to build some of the logic circuits that make up a CPU, Memory, and other devices. We will not describe an entire unit, only a few small parts. The goal is to provide an introductory overview of the concepts. There are many excellent books that cover the details. For example, see [20], [23], or [24] for circuit design details and [28], [31], [34] for CPU architecture design concepts.

Logic circuits can be classiﬁed as either

Combinational Logic Circuits — the output(s) depend only on the input(s) at any speciﬁc time and not on any previous input(s).
Sequential Logic Circuits — the output(s) depend both on previous and current input(s).

An example of the two concepts is a television remote control. You can enter a number and the output (a particular television channel) depends only on the number entered. It does not matter what channels been viewed previously. So the relationship between the input (a number) and the output is combinational.

The remote control also has inputs for stepping either up or down one channel. When using this input method, the channel selected depends on what channel has been previously selected and the sequence of up/down button pushes. The channel up/down buttons illustrate a sequential input/output relationship.

Although a more formal deﬁnition will be given in Section 5.3, this television example also illustrates the concept of state. My television remote control has a button I can push that will show the current channel setting. If I make a note of the beginning channel setting, and keep track of the sequence of channel up and down button pushes, I will know the ending channel setting. It does not matter how I originally got to the beginning channel setting. The channel setting is the state of the channel selection mechanism because it tells me everything I need to know in order to select a new channel by using a sequence of channel up and down button pushes.

5.1 Combinational Logic Circuits

Combinational logic circuits have no memory. The output at any given time depends completely upon the circuit conﬁguration and the input(s).

5.1.1 Adder Circuits

One of the most fundamental operations the ALU must do is to add two bits. We begin with two deﬁnitions. (The reason for the names will become clear later in this section.)

half adder:

A combinational logic device that has two 1-bit inputs, x_i and y_i, and two outputs that are related as shown by the truth table:

x_i	y_i	Carry_i+1	Sum_i

0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

where x_i is the i^th bit of the multiple bit value, x; y_i is the i^th bit of the multiple bit value, y; Sum_i is the i^th bit of the multiple bit value, Sum; Carry_i+1 is the carry from adding the next-lower signiﬁcant bits, x_i, y_i.

full adder:

A combinational logic device that has three 1-bit inputs, Carry_i, x_i, and y_i, and two outputs that are related by the truth table:

Carry_i	x_i	y_i	Carry_i+1	Sum_i

0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

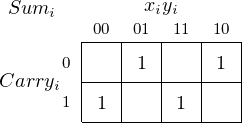
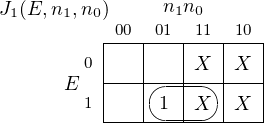
First, let us look at the Karnaugh map for the sum:

PICT

There are no obvious groupings. We can write the function as a sum of product terms from the Karnaugh map.

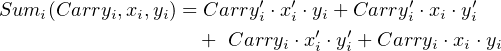Sumi(Carryi,xi,yi) = Carry′i ⋅x′i ⋅yi′ + C′arry ′i ⋅xi ⋅y′i + Carryi ⋅xi ⋅yi + Carryi ⋅xi ⋅yi

(5.1)

In the Karnaugh map for carry:

PICT

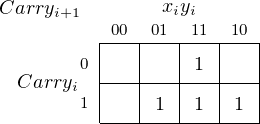
we can see three groupings:

PICT

These groupings yield a three-term function that deﬁnes when Carry_i+1 = 1:

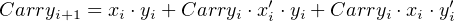Carryi+1 = xi ⋅yi + Carryi ⋅x ′i ⋅yi +Carryi ⋅xi ⋅y′i

(5.2)

Equations 5.1 and 5.2 lead directly to the circuit for an adder in Figure 5.1.

Figure 5.1: An adder circuit.

For a diﬀerent approach, we look at the deﬁnition of half adder. The sum is simply the XOR of the two inputs, and the carry is the AND of the two inputs. This leads to the circuit in Figure 5.2.

Figure 5.2: A half adder circuit.

Instead of using Karnaugh maps, we will perform some algebraic manipulations on Equation 5.1. Using the distribution rule, we can rearrange:

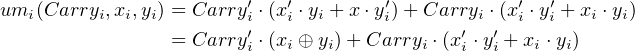′ ′ ′ ′ ′ umi (Carryi,xi,yi) = Carry i′ ⋅(x i ⋅yi +x ⋅yi)+ Carr′yi ⋅′(xi ⋅yi + xi ⋅yi) = Carry i ⋅(xi ⊕ yi)+ Carryi ⋅(xi ⋅yi + xi ⋅yi)

(5.3)

Let us manipulate the last product term in Equation 5.3.

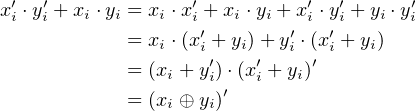x′i ⋅y′i + xi ⋅yi = xi ⋅x′i + xi ⋅yi + x′i ⋅y′i + yi ⋅y′i = x ⋅(x′+ y)+ y′⋅(x′+ y ) i i′ i′ i ′ i i = (xi + yi)⋅(xi + yi) = (xi ⊕ yi)′

Thus,

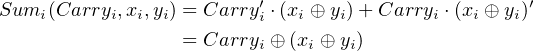′ ′ Sumi (Carryi,xi,yi) = Carryi ⋅(xi ⊕ yi)+ Carryi ⋅(xi ⊕ yi) = Carryi ⊕ (xi ⊕ yi)

(5.4)

Similarly, we can rewrite Equation 5.2:

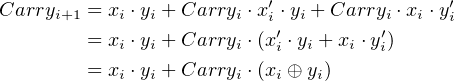′ ′ Carryi+1 = xi ⋅yi + Carryi ⋅x i′ ⋅yi +Carryi′ ⋅xi ⋅yi = xi ⋅yi + Carryi ⋅(xi ⋅yi + xi ⋅yi) = xi ⋅yi + Carryi ⋅(xi ⊕ yi)

(5.5)

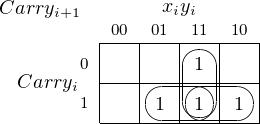
You should be able to see two other possible groupings on this Karnaugh map and may wonder why they are not circled here. The two ungrouped minterms, Carry_i ⋅ x_i′⋅ y_i and Carry_i ⋅ x_i ⋅ y_i′, form a pattern that suggests an exclusive or operation.

Notice that the ﬁrst product term in Equation 5.5, x_i ⋅ y_i, is generated by the Carry portion of a half-adder, and that the exclusive or portion, x_i ⊕y_i, of the second product term is generated by the Sum portion. A logic gate implementation of a full adder is shown in Figure 5.3.

Figure 5.3: Full adder using two half adders.

You can see that it is implemented using two half adders and an OR gate. And now you understand the terminology “half adder” and “full adder.”

We cannot say which of the two adder circuits, Figure 5.1 or Figure 5.3, is better from just looking at the logic circuits. Good engineering design depends on many factors, such as how each logic gate is implemented, the cost of the logic gates and their availability, etc. The two designs are given here to show that diﬀerent approaches can lead to diﬀerent, but functionally equivalent, designs.

5.1.2 Ripple-Carry Addition/Subtraction Circuits

An n-bit adder can be implemented with n full adders. Figure 5.4 shows a 4-bit adder.

Figure 5.4: Four-bit adder.

Addition begins with the full adder on the right receiving the two lowest-order bits, x₀ and y₀. Since this is the lowest-order bit there is no carry and c₀ = 0. The bit sum is s₀, and the carry from this addition, c₁, is connected to the carry input of the next full adder to the left, where it is added to x₁ and y₁.

So the i^th full adder adds the two i^th bits of the operands, plus the carry (which is either 0 or 1) from the (i − 1)^th full adder. Thus, each full adder handles one bit (often referred to as a “slice”) of the total width of the values being added, and the carry “ripples” from the lowest-order place to the highest-order.

The ﬁnal carry from the highest-order full adder, c₄ in the 4-bit adder of Figure 5.4, is stored in the CF bit of the Flags register (see Section 6.2). And the exclusive or of the ﬁnal carry and penultimate carry, c₄ ⊕ c₃ in the 4-bit adder of Figure 5.4, is stored in the OF bit.

Recall that in the 2’s complement code for storing integers a number is negated by taking its 2’s complement. So we can subtract y from x by doing:

x − y = x + (2’s complement of y) = x + [(y’s bits ﬂipped)+ 1]

(5.6)

Thus, subtraction can be performed with our adder in Figure 5.4 if we complement each y_i and set the initial carry in to 1 instead of 0. Each y_i can be complemented by XOR-ing it with 1. This leads to the 4-bit circuit in Figure 5.5 that will add two 4-bit numbers when func = 0 and subtract them when func = 1.

Figure 5.5: Four-bit adder/subtracter.

There is, of course, a time delay as the sum is computed from right to left. The computation time can be signiﬁcantly reduced through more complex circuit designs that pre-compute the carry.

5.1.3 Decoders

Each instruction must be decoded by the CPU before the instruction can be carried out. In the x86-64 architecture the instruction for copying the 64 bits of one register to another register is

0100 0s0d 1000 1001 11ss sddd

where “ssss” speciﬁes the source register and “dddd” speciﬁes the destination register. (Yes, the bits that specify the registers are distributed through the instruction in this manner. You will learn more about this seemingly odd coding pattern in Chapter 9.) For example,

0100 0001 1000 1001 1100 0101

causes the ALU to copy the 64-bit value in register 0000 to register 1101. You will see in Chapter 9 that this instruction is written in assembly language as:

movq %rax, %r13

The Control Unit must select the correct two registers based on these two 4-bit patterns in the instruction. It uses a decoder circuit to perform this selection.

decoder:: A device with n binary inputs and 2ⁿ binary outputs. Each bit pattern at the input causes exactly one of the 2ⁿ to equal 1.

A decoder can be thought of as converting an n-bit input to a 2ⁿ output. But while the input can be an arbitrary bit pattern, each corresponding output value has only one bit set to 1.

In some applications not all the 2ⁿ outputs are used. For example, Table 5.1 is a truth table that shows how a decoder can be used to convert a BCD value to its corresponding decimal numeral display.

input				display
x₃	x₂	x₁	x₀	′9′	′8′	′7′	′6′	′5′	′4′	′3′	′2′	′1′	′0′

0	0	0	0	0	0	0	0	0	0	0	0	0	1
0	0	0	1	0	0	0	0	0	0	0	0	1	0
0	0	1	0	0	0	0	0	0	0	0	1	0	0
0	0	1	1	0	0	0	0	0	0	1	0	0	0
0	1	0	0	0	0	0	0	0	1	0	0	0	0
0	1	0	1	0	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	0	1	0	0	0	0	0	0
0	1	1	1	0	0	1	0	0	0	0	0	0	0
1	0	0	0	0	1	0	0	0	0	0	0	0	0
1	0	0	1	1	0	0	0	0	0	0	0	0	0

Table 5.1: BCD decoder. The 4-bit input causes the numeral with a 1 in its column to be displayed.

A 1 in a “display” column means that is the numeral that is selected by the corresponding 4-bit input value. There are six other possible outputs corresponding to the input values 1010 – 1111. But these input values are illegal in BCD, so these outputs are simply ignored.

It is common for decoders to have an additional input that is used to enable the output. The truth table in Table 5.2 shows a decoder with a 3-bit input, an enable line, and an 8-bit (2³) output.

enable	x₂	x₁	x₀	y₇	y₆	y₅	y₄	y₃	y₂	y₁	y₀

0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0	0
0	1	0	1	0	0	0	0	0	0	0	0
0	1	1	0	0	0	0	0	0	0	0	0
0	1	1	1	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	1
1	0	0	1	0	0	0	0	0	0	1	0
1	0	1	0	0	0	0	0	0	1	0	0
1	0	1	1	0	0	0	0	1	0	0	0
1	1	0	0	0	0	0	1	0	0	0	0
1	1	0	1	0	0	1	0	0	0	0	0
1	1	1	0	0	1	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0	0

Table 5.2: Truth table for a 3 × 8 decoder with enable. If enable = 0, y = 0. If enable = 1, x = i ⇒ y_i = 1 and y_j = 0 for all j≠i.

The output is 0 whenever enable = 0. When enable = 1, the i^th output bit is 1 if and only if the binary value of the input is equal to i. For example, when enable = 1 and x = 011₂, y = 00001000₂. That is,

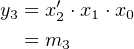′ y3 = x 2 ⋅x1 ⋅x0 = m3

(5.7)

This clearly generalizes such that we can give the following description of a decoder:

For n input bits (excluding an enable bit) there are 2ⁿ output bits.
The i^th output bit is equal to the i^th minterm for the n input bits.

The 3 × 8 decoder speciﬁed in Table 5.2 can be implemented with 4-input AND gates as shown in Figure 5.6.

Figure 5.6: Circuit for a 3 × 8 decoder with enable.

Decoders are more versatile than it might seem at ﬁrst glance. Each possible input can be seen as a minterm. Since each output is one only when a particular minterm evaluates to one, a decoder can be viewed as a “minterm generator.” We know that any logical expression can be represented as the OR of minterms, so it follows that we can implement any logical expression by ORing the output(s) of a decoder.

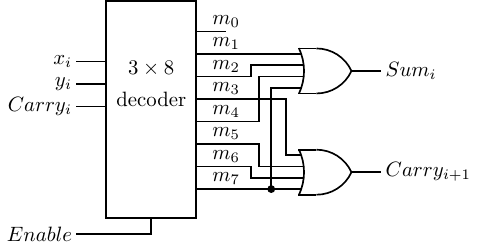
For example, let us rewrite Equation 5.1 for the Sum expression of a full adder using minterm notation (see Section 4.3.2):

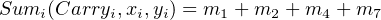Sumi (Carryi,xi,yi) = m1 + m2 + m4 + m7

(5.8)

And for the Carry expression:

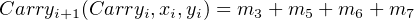Carryi+1 (Carryi,xi,yi) = m3 + m5 + m6 + m7

(5.9)

where the subscripts on x, y, and Carry refer to the bit slice and the subscripts on m are part of the minterm notation. We can implement a full adder with a 3 × 8 decoder and two 4-input OR gates, as shown in Figure 5.7.

Figure 5.7: Full adder implemented with 3×8 decoder. This is for one bit slice. An n-bit adder would require n of these circuits.

5.1.4 Multiplexers

There are many places in the CPU where one of several signals must be selected to pass onward. For example, as you will see in Chapter 9, a value to be added by the ALU may come from a CPU register, come from memory, or actually be stored as part of the instruction itself. The device that allows this selection is essentially a switch.

multiplexer:: A device that selects one of multiple inputs to be passed on as the output based on one or more selection lines. Up to 2ⁿ inputs can be selected by n selection lines. Also called a mux.

Figure 5.8 shows a multiplexer that can switch between two diﬀerent inputs, x and y. The select input, s, determines which of the sources, either x or y, is passed on to the output. The action of this 2-way multiplexer is most easily seen in a truth table:

s	Output

1	x
0	y

Figure 5.8: A 2-way multiplexer.

Here is a truth table for a multiplexer that can switch between four inputs, w, x, y, and z:

s₁	s₀	Output

0	0	w
0	1	x
1	0	y
1	1	z

That is,

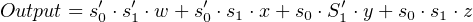Output = s′0 ⋅s′1 ⋅w +s′0 ⋅s1 ⋅x+ s0 ⋅S1′⋅y+ s0 ⋅s1 ⋅z

(5.10)

which is implemented as shown in Figure 5.9.

Figure 5.9: A 4-way multiplexer.

The symbol for this multiplexer is shown in Figure 5.10.

Figure 5.10: Symbol for a 4-way multiplexer.

Notice that the selection input, s, must be 2 bits in order to select between four inputs. In general, a 2ⁿ-way multiplexer requires an n-bit selection input.

5.2 Programmable Logic Devices

Combinational logic circuits can be constructed from programmable logic devices (PLDs). The general idea is illustrated in Figure 5.11 for two input variables and two output functions of these variables.

Figure 5.11: Simpliﬁed circuit for a programmable logic array. The “S” shaped line at the inputs to each gate represent fuses. The fuses are “blown” to remove that input.

Each of the input variables, both in its uncomplemented and complemented form, are inputs to AND gates through fuses. (The “S” shaped lines in the circuit diagram represent fuses.) The fuses can be “blown” or left in place in order to program each AND gate to output a product. Since every input, plus its complement, is input to each AND gate, any of the AND gates can be programmed to output a minterm.

The products produced by the array of AND gates are all connected to OR gates, also through fuses. Thus, depending on which OR-gate fuses are left in place, the output of each OR gate is a sum of products. There may be additional logic circuitry to select between the diﬀerent outputs. We have already seen that any Boolean function can be expressed as a sum of products, so this logic device can be programmed by “blowing” the fuses to implement any Boolean function.

PLDs come in many conﬁgurations. Some are pre-programmed at the time of manufacture. Others are programmed by the manufacturer. And there are types that can be programmed by a user. Some can even be erased and reprogrammed. Programming technologies range from specifying the manufacturing mask (for the pre-programmed devices) to inexpensive electronic programming systems. Some devices use “antifuses” instead of fuses. They are normally open. Programming such devices consists of completing the connection instead of removing it.

There are three general categories of PLDs:

Programmable Logic Array (PLA):: Both the AND gate plane and the OR gate plane are programmable.
Read Only Memory (ROM):: Only the OR gate plane is programmable.
Programmable Array Logic (PAL):: Only the AND gate plane is programmable.

We will now look at each category in more detail.

5.2.1 Programmable Logic Array (PLA)

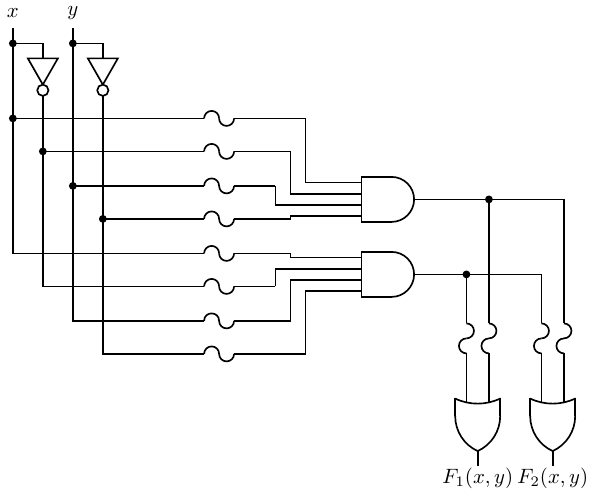
Programmable logic arrays are typically larger than the one shown in Figure 5.11, which is already complicated to draw. Figure 5.12 shows how PLAs are typically diagrammed.

Figure 5.12: Programmable logic array schematic. The horizontal lines to the AND gate inputs represent multiple wires — one for each input variable and its complement. The vertical lines to the OR gate inputs also represent multiple wires — one for each AND gate output. The dots represent connections.

This diagram deserves some explanation. Note in Figure 5.11 that each input variable and its complement is connected to the inputs of all the AND gates through a fuse. The AND gates have multiple inputs — one for each variable and its complement. Thus, the horizontal line leading to the inputs of the AND gates represent multiple wires. The diagram of Figure 5.12 has four input variables. So each AND gate has eight inputs, and the horizontal lines each represent the eight wires coming from the inputs and their complements.

The dots at the intersections of the vertical and horizontal line represent places where the fuses have been left intact. For example, the three dots on the topmost horizontal line indicate that there are three inputs to that AND gate The output of the topmost AND gate is

w ′ ⋅y⋅z

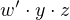Referring again to Figure 5.11, we see that the output from each AND gate is connected to each of the OR gates. Therefore, the OR gates also have multiple inputs — one for each AND gate — and the vertical lines leading to the OR gate inputs represent multiple wires. The PLA in Figure 5.12 has been programmed to provide the three functions:

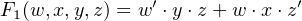′ ′ F1(w,x,y,z) = w ⋅y⋅z + w ⋅x ⋅z

(5.11)

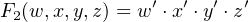F2(w, x,y,z) = w′ ⋅x′ ⋅y′ ⋅z′

(5.12)

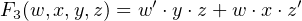′ ′ F3(w,x,y,z) = w ⋅y⋅z + w ⋅x ⋅z

(5.13)

5.2.2 Read Only Memory (ROM)

Read only memory can be implemented as a programmable logic device where only the OR plane can be programmed. The AND gate plane is wired to provide all the minterms. Thus, the inputs to the ROM can be thought of as addresses. Then the OR gate plane is programmed to provide the bit pattern at each address.

For example, the ROM diagrammed in Figure 5.13 has two inputs, a₁ and a₀.

Figure 5.13: Eight-byte Read Only Memory (ROM). The “×” connections represent permanent connections. Each AND gate can be thought of as producing an address. The eight OR gates produce one byte. The connections (dots) in the OR plane represent the bit pattern stored at the address.

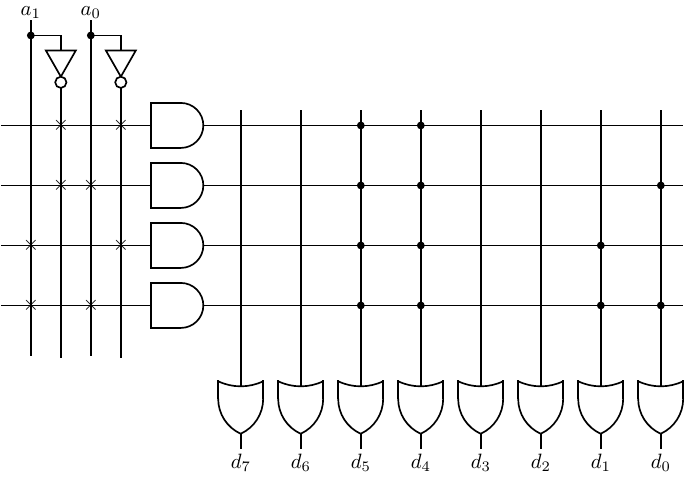
The AND gates are wired to give the minterms:

minterm	address

a₁′a₀′	00
a₁′a₀	01
a₁a₀′	10
a₁a₀	11

And the OR gate plane has been programmed to store the four characters (in ASCII code):

minterm	address	contents

a₁′a₀′	00	′0′
a₁′a₀	01	′1′
a₁a₀′	10	′2′
a₁a₀	11	′3′

You can see from this that the terminology “Read Only Memory” is perhaps a bit misleading. It is actually a combinational logic circuit. Strictly speaking, memory has a state that can be changed by inputs. (See Section 5.3.)

5.2.3 Programmable Array Logic (PAL)

In a Programmable Array Logic (PAL) device, each OR gate is permanently wired to a group of AND gates. Only the AND gate plane is programmable. The PAL diagrammed in Figure 5.14 has four inputs. It provides two outputs, each of which can be the sum of up to four products. The “×” connections in the OR gate plane show that the top four AND gates are summed to produce F₁ and the lower four to produce F₂. The AND gate plane in this ﬁgure has been programmed to produce the two functions:

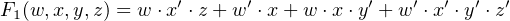′ ′ ′ ′ ′ ′ ′ F1(w,x,y,z) = w ⋅x ⋅z + w ⋅x+ w ⋅x⋅y + w ⋅x ⋅y ⋅z

(5.14)

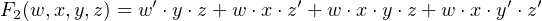F (w,x,y,z) = w′ ⋅y ⋅z + w ⋅x⋅z′ + w ⋅x⋅y ⋅z + w ⋅x⋅y′ ⋅z′ 2

(5.15)

Figure 5.14: Two-function Programmable Array Logic (PAL). The “×” connections represent permanent connections. Each AND gate can be thought of as producing an address. The eight OR gates produce one byte. The connections (dots) in the OR plane represent the bit pattern stored at the address.

5.3 Sequential Logic Circuits

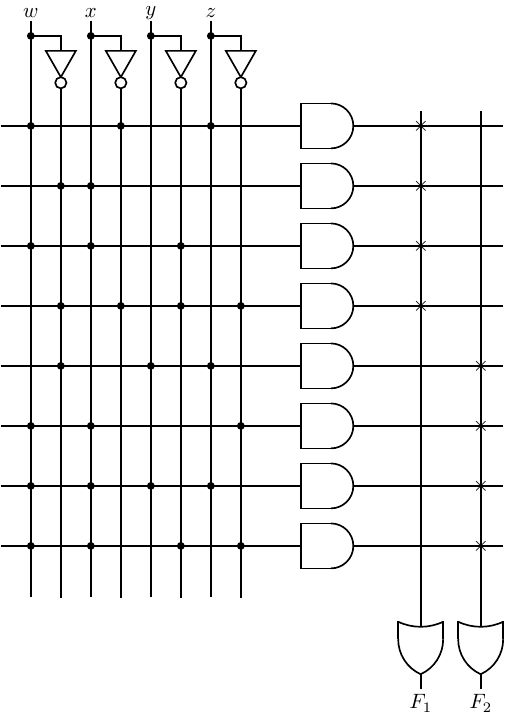
Combinational circuits (Section 5.1) are instantaneous (except for the time required for the electronics to settle). Their output depends only on the input at the time the output is observed. Sequential logic circuits, on the other hand, have a time history. That history is summarized by the current state of the circuit.

state:

The state of a system is the description of the system such that knowing

the state at time t₀, and
the input(s) from time t₀ through time t₁,

uniquely determines

the state at time t₁, and
the output(s) from time t₀ through time t₁.

This deﬁnition means that knowing the state of a system at a given time tells you everything you need to know in order to specify its behavior from that time on. How it got into this state is irrelevant.

This deﬁnition implies that the system has memory in which the state is stored. Since there are a ﬁnite number of states, the term ﬁnite state machine(FSM) is commonly used. Inputs to the system can cause the state to change.

If the output(s) depend only on the state of the FSM, it is called a Moore machine. And if the output(s) depend on both the state and the current input(s), it is called a Mealy machine.

The most commonly used sequential circuits are synchronous — their action is controlled by a sequence of clock pulses. The clock pulses are created by a clock generator circuit. The clock pulses are applied to all the sequential elements, thus causing them to operate in synchrony.

Asynchronous sequential circuits are not based on a clock. They depend upon a timing delay built into the individual elements. Their behavior depends upon the order in which inputs are applied. Hence, they are diﬃcult to analyze and will not be discussed in this book.

5.3.1 Clock Pulses

A clock signal is typically a square wave that alternates between the 0 and 1 levels as shown in Figure 5.15 The amount of time spent at each level may be unequal. Although not a requirement, the timing pattern is usually uniform.

PICT

Figure 5.15: Clock signals. (a) For level-triggered circuits. (b) For positive-edge triggering. (c) For negative-edge triggering.

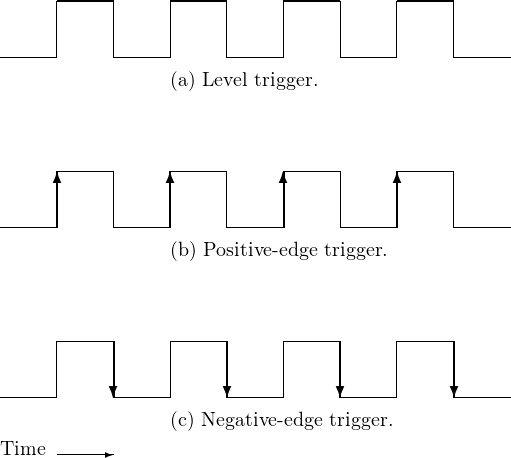
In Figure 5.15(a), the circuit operations take place during the entire time the clock is at the 1 level. As will be explained below, this can lead to unreliable circuit behavior. In order to achieve more reliable behavior, most circuits are designed such that a transition of the clock signal triggers the circuit elements to start their respective operations. Either a positive-going (Figure 5.15(b)) or negative-going (Figure 5.15(c)) transition may be used. The clock frequency must be slow enough such that all the circuit elements have time to complete their operations before the next clock transition (in the same direction) occurs.

5.3.2 Latches

A latch is a storage device that can be in one of two states. That is, it stores one bit. It can be constructed from two or more gates connected such that feedback maintains the state as long as power is applied. The most fundamental latch is the SR (Set-Reset).

A simple implementation using NOR gates is shown in Figure 5.16.

Figure 5.16: NOR gate implementation of an SR latch.

When Q = 1 (⇔ Q′ = 0) it is in the Set state. When Q = 0 (⇔ Q′ = 1) it is in the Reset state.

There are four possible input combinations.

S = 0, R = 0: Keep current state.

If Q = 0 and Q′ = 1, the output of the upper NOR gate is (0 + 0)′ = 1, and the output of the lower NOR gate is (1 + 0)′ = 0.

If Q = 1 and Q′ = 0, the output of the upper NOR gate is (0 + 1)′ = 0, and the output of the lower NOR gate is (0 + 0)′ = 1.

Thus, the cross feedback between the two NOR gates maintains the state — Set or Reset — of the latch.

S = 1, R = 0: Set.

If Q = 1 and Q′ = 0, the output of the upper NOR gate is (1 + 1)′ = 0, and the output of the lower NOR gate is (0 + 0)′ = 1. The latch remains in the Set state.

If Q = 0 and Q′ = 1, the output of the upper NOR gate is (1 + 0)′ = 0. This is fed back to the input of the lower NOR gate to give (0 + 0)′ = 1. The feedback from the output of the lower NOR gate to the input of the upper keeps the output of the upper NOR gate at (1 + 1)′ = 0. The latch has moved into the Set state.

S = 0, R = 1: Reset.

If Q = 1 and Q′ = 0, the output of the lower NOR gate is (0 + 1)′ = 0. This causes the output of the upper NOR gate to become (0 + 0)′ = 1. The feedback from the output of the upper NOR gate to the input of the lower keeps the output of the lower NOR gate at (1 + 1)′ = 0. The latch has moved into the Reset state.

If Q = 0 and Q′ = 1, the output of the lower NOR gate is (1 + 1)′ = 0, and the output of the upper NOR gate is (0 + 0)′ = 1. The latch remains in the Reset state.

S = 1, R = 1: Not allowed.

If Q = 0 and Q′ = 1, the output of the upper NOR gate is (1 + 0)′ = 0. This is fed back to the input of the lower NOR gate to give (0 + 1)′ = 0 as its output. The feedback from the output of the lower NOR gate to the input of the upper maintains its output as (1 + 0)′ = 0. Thus, Q = Q′ = 0, which is not allowed.

If Q = 1 and Q′ = 0, the output of the lower NOR gate is (0 + 1)′ = 0. This is fed back to the input of the upper NOR gate to give (1 + 0)′ = 0 as its output. The feedback from the output of the upper NOR gate to the input of the lower maintains its output as (0 + 1)′ = 0. Thus, Q = Q′ = 0, which is not allowed.

The state table in Table 5.3 summarizes the behavior of a NOR-based SR latch.

		Current	Next
S	R	State	State

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	X
1	1	1	X

Table 5.3: SR latch state table. “X” indicates an indeterminate state. A circuit using this latch must be designed to prevent this input combination.

The inputs to a NOR-based SR latches are normally held at 0, which maintains the current state, Q. Its current state is available at the output. Momentarily changing S or R to 1 causes the state to change to Set or Reset, respectively, as shown in the Q_next column.

Notice that placing 1 on both the Set and Reset inputs at the same time causes a problem. Then the outputs of both NOR gates would become 0. In other words, Q = Q′ = 0, which is logically impossible. The circuit design must be such to prevent this input combination.

The behavior of an SR latch can also be shown by the state diagram in Figure 5.17

Figure 5.17: State diagram for an SR latch. There are two possible inputs, 00 or 01, that cause the latch to remain in state 0. Similarly, 00 or 10 cause it to remain in state 1. Since the output is simply the state, it is not shown in this state diagram. Notice that the input 11 is not allowed, so it is not shown on the diagram.

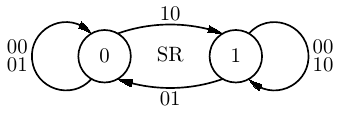
A state diagram is a directed graph. The circles show the possible states. Lines with arrows show the possible transitions between the states and are labeled with the input that causes the transition.

The two circles in Figure 5.17 show the two possible states of the SR latch — 0 or 1. The labels on the lines show the two-bit inputs, SR, that cause each state transition. Notice that when the latch is in state 0 there are two possible inputs, SR = 00 and SR = 01, that cause it to remain in that state. Similarly, when it is in state 1 either of the two inputs, SR = 00 or SR = 10, cause it to remain in that state.

The output of the SR latch is simply the state so is not shown separately on this state diagram. In general, if the output of a circuit is dependent on the input, it is often shown on the directed lines of the state diagram in the format “input/output.” If the output is dependent on the state, it is more common to show it in the corresponding state circle in “state/output” format.

NAND gates are more commonly used than NOR gates, and it is possible to build an SR latch from NAND gates. Recalling that NAND and NOR have complementary properties, we will think ahead and use S′ and R′ as the inputs, as shown in Figure 5.18.

Figure 5.18: NAND gate implementation of an S’R’ latch.

Consider the four possible input combinations.

S’ = 1, R’ = 1: Keep current state.

If Q = 0 and Q′ = 1, the output of the upper NAND gate is (1 ⋅ 1)′ = 0, and the output of the lower NAND gate is (0 ⋅ 1)′ = 1.

If Q = 1 and Q′ = 0, the output of the upper NAND gate is (1 ⋅ 0)′ = 1, and the output of the lower NAND gate is (1 ⋅ 1)′ = 0.

Thus, the cross feedback between the two NAND gates maintains the state — Set or Reset — of the latch.

S’ = 0, R’ = 1: Set.

If Q = 1 and Q′ = 0, the output of the upper NAND gate is (0 ⋅ 0)′ = 1, and the output of the lower NAND gate is (1 ⋅ 1)′ = 0. The latch remains in the Set state.

If Q = 0 and Q′ = 1, the output of the upper NAND gate is (0 ⋅ 1)′ = 1. This causes the output of the lower NAND gate to become (1 ⋅ 1)′ = 0. The feedback from the output of the lower NAND gate to the input of the upper keeps the output of the upper NAND gate at (0 ⋅ 0)′ = 1. The latch has moved into the Set state.

S’ = 1, R’ = 0: Reset.

If Q = 0 and Q′ = 1, the output of the lower NAND gate is (0 ⋅ 0)′ = 1, and the output of the upper NAND gate is (1 ⋅ 1)′ = 0. The latch remains in the Reset state.

If Q = 1 and Q′ = 0, the output of the lower NAND gate is (1 ⋅ 0)′ = 1. This is fed back to the input of the upper NAND gate to give (1 ⋅ 1)′ = 0. The feedback from the output of the upper NAND gate to the input of the lower keeps the output of the lower NAND gate at (0 ⋅ 0)′ = 1. The latch has moved into the Reset state.

S’ = 0, R’ = 0: Not allowed.

If Q = 0 and Q′ = 1, the output of the upper NAND gate is (0 ⋅ 1)′ = 1. This is fed back to the input of the lower NAND gate to give (1 ⋅ 0)′ = 1 as its output. The feedback from the output of the lower NAND gate to the input of the upper maintains its output as (0 ⋅ 0)′ = 1. Thus, Q = Q′ = 1, which is not allowed.

If Q = 1 and Q′ = 0, the output of the lower NAND gate is (1 ⋅ 0)′ = 1. This is fed back to the input of the upper NAND gate to give (0 ⋅ 1)′ = 1 as its output. The feedback from the output of the upper NAND gate to the input of the lower maintains its output as (1 ⋅ 1)′ = 0. Thus, Q = Q′ = 1, which is not allowed.

Figure 5.19 shows the behavior of a NAND-based S’R’ latch. The inputs to a NAND-based S’R’ latch are normally held at 1, which maintains the current state, Q. Its current state is available at the output. Momentarily changing S′ or R′ to 0 causes the state to change to Set or Reset, respectively, as shown in the “Next State” column.

		Current	Next
S′	R′	State	State

1	1	0	0
1	1	1	1
1	0	0	0
1	0	1	0
0	1	0	1
0	1	1	1
0	0	0	X
0	0	1	X

Figure 5.19: State table and state diagram for an S’R’ latch. There are two possible inputs, 11 or 10, that cause the latch to remain in state 0. Similarly, 11 or 01 cause it to remain in state 1. Since the output is simply the state, it is not shown in this state diagram. Notice that the input 00 is not allowed, so it is not shown on the diagram.

Notice that placing 0 on both the Set and Reset inputs at the same time causes a problem. Then the outputs of both NOR gates would become 0. In other words, Q = Q′ = 0, which is logically impossible. The circuit design must be such to prevent this input combination.

So the S’R’ latch implemented with two NAND gates can be thought of as the complement of the NOR gate SR latch. The state is maintained by holding both S′ and ′ at 1. S′ = 0 causes the state to be 1 (Set), and R′ = 0 causes the state to be 0 (Reset). Using S′ and R′ as the activating signals are usually called active-low signals.

You have already seen that ones and zeros are represented by either a high or low voltage in electronic logic circuits. A given logic device may be activated by combinations of the two voltages. To show which is used to cause activation at any given input, the following deﬁnitions are used:

active-high signal:: The higher voltage represents 1.
active-low signal:: The lower voltage represents 1.

Warning! The deﬁnitions of active-high versus active-low signals vary in the literature. Make sure that you and the people you are working with have a clear agreement on the deﬁnitions you are using.

An active-high signal can be connected to an active-low input, but the hardware designer must take the diﬀerence into account. For example, say that the required logical input is 1 to an active-low input. Since it is active-low, that means the required voltage is the lower of the two. If the signal to be connected to this input is active-high, then a logical 1 is the higher of the two voltages. So this signal must ﬁrst be complemented in order to be interpreted as a 1 at the active-low input.

We can get better control over the SR latch by adding two NAND gates to provide a Control input, as shown in Figure 5.20.

Figure 5.20: SR latch with Control input.

In this circuit the outputs of both the control NAND gates remain at 1 as long as Control = 0. Table 5.4 shows the state behavior of the SR latch with control.

			Current	Next
Control	S	R	State	State

0	−	−	0	0
0	−	−	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	X
1	1	1	1	X

Table 5.4: SR latch with Control state table. “–” indicates that the value does not matter. “X” indicates an indeterminate state. A circuit using this latch must be designed to prevent this input combination.

It is clearly better if we could ﬁnd a design that eliminates the possibility of the “not allowed” inputs. Table 5.5 is a state table for a D latch. It has two inputs, one for control, the other for data, D. D = 1 sets the latch to 1, and D = 0 resets it to 0.

		Current	Next
Control	D	State	State

0	−	0	0
0	−	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Table 5.5: D latch with Control state table. “–” indicates that the value does not matter.

The D latch can be implemented as shown in Figure 5.21.

Figure 5.21: D latch constructed from an SR latch.

The one data input, D, is fed to the “S” side of the SR latch; the complement of the data value is fed to the “R” side.

Now we have a circuit that can store one bit of data, using the D input, and can be synchronized with a clock signal, using the Control input. Although this circuit is reliable by itself, the issue is whether it is reliable when connected with other circuit elements. The D signal almost certainly comes from an interconnection of combinational and sequential logic circuits. If it changes while the Control is still 1, the state of the latch will be changed.

Each electronic element in a circuit takes time to activate. It is a very short period of time, but it can vary slightly depending upon precisely how the other logic elements are interconnected and the state of each of them when they are activated. The problem here is that the Control input is being used to control the circuit based on the clock signal level. The clock level must be maintained for a time long enough to allow all the circuit elements to complete their activity, which can vary depending on what actions are being performed. In essence, the circuit timing is determined by the circuit elements and their actions instead of the clock. This makes it very diﬃcult to achieve a reliable design.

It is much easier to design reliable circuits if the time when an activity can be triggered is made very short. The solution is to use edge-triggered logic elements. The inputs are applied and enough time is allowed for the electronics to settle. Then the next clock transition activates the circuit element. This scheme provides concise timing under control of the clock instead of timing determined more or less by the particular circuit design.

5.3.3 Flip-Flops

Although the terminology varies somewhat in the literature, it is generally agreed that (see Figure 5.15.):

A latch uses a level based clock signal.
A ﬂip-ﬂop is triggered by a clock signal edge.

At each “tick” of the clock, there are four possible actions that might be taken on a single bit — store 0, store 1, complement the bit (also called toggle), or leave it as is.

A D ﬂip-ﬂop is a common device for storing a single bit. We can turn the D latch into a D ﬂip-ﬂop by using two D latches connected in a master/slave conﬁguration as shown in Figure 5.22.

Figure 5.22: D ﬂip-ﬂop, positive-edge triggering.

Let us walk through the operation of this circuit.

The bit to be stored, 0 or 1, is applied to the D input of the Master D latch. The clock signal is applied to the CK input. It is normally 0. When the clock signal makes a transition from 0 to 1, the Master D latch will either Reset or Set, following the D input of 0 or 1, respectively.

While the CK input is at the 1 level, the control signal to the Slave D latch is 1, which deactivates this latch. Meanwhile, the output of this ﬂip-ﬂop, the output of the Slave D latch, is probably connected to the input of another circuit, which is activated by the same CK. Since the state of the Slave does not change during this clock half-cycle, the second circuit has enough time to read the current state of the ﬂip-ﬂop connected to its input. Also during this clock half-cycle, the state of the Master D latch has ample time to settle.

When the CK input transitions back to the 0 level, the control signal to the Master D latch becomes 1, deactivating it. At the same time, the control input to the Slave D latch goes to 0, thus activating the Slave D latch to store the appropriate value, 0 or 1. The new input will be applied to the Slave D latch during the second clock half-cycle, after the circuit connected to its output has had suﬃcient time to read its previous state. Thus, signals travel along a path of logic circuits in lock step with a clock signal.

There are applications where a ﬂip-ﬂop must be set to a known value before the clocking begins. Figure 5.23 shows a D ﬂip-ﬂop with an asynchronous preset input added to it.

Figure 5.23: D ﬂip-ﬂop, positive-edge triggering with asynchronous preset.

When a 1 is applied to the PR input, Q becomes 1 and Q′ 0, regardless of what the other inputs are, even CLK. It is also common to have an asynchronous clear input that sets the state (and output) to 0.

There are more eﬃcient circuits for implementing edge-triggered D ﬂip-ﬂops, but this discussion serves to show that they can be constructed from ordinary logic gates. They are economical and eﬃcient, so are widely used in very large scale integration circuits. Rather than draw the details for each D ﬂip-ﬂop, circuit designers use the symbols shown in Figure 5.24.

Figure 5.24: Symbols for D ﬂip-ﬂops. Includes asynchronous clear (CLR) and preset (PR). (a) Positive-edge triggering; (b) Negative-edge triggering.

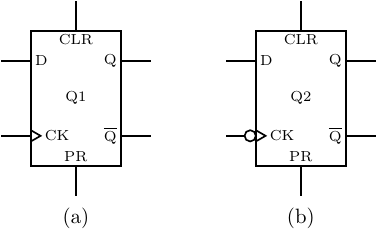
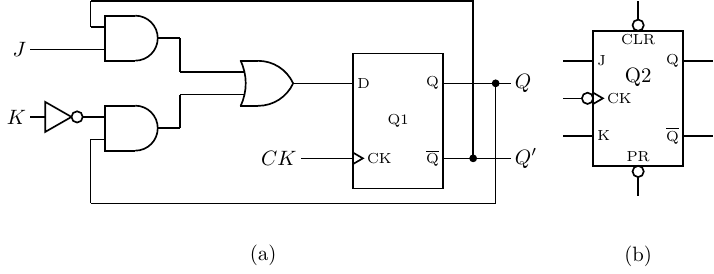
The various inputs and outputs are labeled in this ﬁgure. Hardware designers typically use Q instead of Q′. It is common to label the circuit as “Qn,” with n = 1, 2,…for identiﬁcation. The small circle at the clock input in Figure 5.24(b) means that this D ﬂip-ﬂop is triggered by a negative-going clock transition. The D ﬂip-ﬂop circuit in Figure 5.22 can be changed to a negative-going trigger by simply removing the ﬁrst NOT gate at the CK input.

The ﬂip-ﬂop that simply complements its state, a T ﬂip-ﬂop, is easily constructed from a D ﬂip-ﬂop. The state table and state diagram for a T ﬂip-ﬂop are shown in Figure 5.25.

	Current	Next
T	State	State

0	0	0
0	1	1
1	0	1
1	1	0

Figure 5.25: T ﬂip-ﬂop state table and state diagram. Each clock tick causes a state transition, with the next state depending on the current state and the value of the input, T.

To determine the value that must be presented to the D ﬂip-ﬂop in order to implement a T ﬂip-ﬂop, we add a column for D to the state table as shown in Table 5.6.

	Current	Next
T	State	State	D

0	0	0	0
0	1	1	1
1	0	1	1
1	1	0	0

Table 5.6: T ﬂip-ﬂop state table showing the D ﬂip-ﬂop input required to place the T ﬂip-ﬂop in the next state.

By simply looking in the “Next State” column we can see what the input to the D ﬂip-ﬂop must be in order to obtain the correct state. These values are entered in the D column. (We will generalize this design procedure in Section 5.4.)

From Table 5.6 it is easy to write the equation for D:

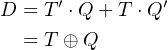′ ′ D = T ⋅Q + T ⋅Q = T ⊕Q

(5.16)

The resulting design for the T ﬂip-ﬂop is shown in Figure 5.26.

Figure 5.26: T ﬂip-ﬂop. (a) Circuit using a D ﬂip-ﬂop. (b) Symbol for a T ﬂip-ﬂop.

Implementing all four possible actions — set, reset, keep, toggle — requires two inputs, J and K, which leads us to the JK ﬂip-ﬂop. The state table and state diagram for a JK ﬂip-ﬂop are shown in Figure 5.27.

		Current	Next
J	K	State	State

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Figure 5.27: JK ﬂip-ﬂop state table and state diagram.

In order to determine the value that must be presented to the D ﬂip-ﬂop we add a column for D to the state table as shown in Table 5.7.

		Current	Next
J	K	State	State	D

0	0	0	0	0
0	0	1	1	1
0	1	0	0	0
0	1	1	0	0
1	0	0	1	1
1	0	1	1	1
1	1	0	1	1
1	1	1	0	0

Table 5.7: JK ﬂip-ﬂop state table showing the D ﬂip-ﬂop input required to place the JK ﬂip-ﬂop in the next state.

shows what values must be input to the D ﬂip-ﬂop. From this it is easy to write the equation for D:

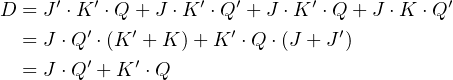′ ′ ′ ′ ′ ′ D = J ⋅K′ ⋅Q +′ J ⋅K ⋅Q′+ J ⋅K ⋅Q′ +J ⋅K ⋅Q = J ⋅Q ⋅(K +K )+ K ⋅Q ⋅(J + J ) = J ⋅Q′ + K ′ ⋅Q

(5.17)

Thus, a JK ﬂip-ﬂop can be constructed from a D ﬂip-ﬂop as shown in Figure 5.28.

Figure 5.28: JK ﬂip-ﬂop. (a) Circuit using a D ﬂip-ﬂop. (b) Symbol for a JK ﬂip-ﬂop with asynchronous CLR and PR inputs.

5.4 Designing Sequential Circuits

We will now consider a more general set of steps for designing sequential circuits.¹ Design in any ﬁeld is usually an iterative process, as you have no doubt learned from your programming experience. You start with a design, analyze it, and then reﬁne the design to make it faster, less expensive, etc. After gaining some experience, the design process usually requires fewer iterations.

The following steps form a good method for a ﬁrst working design:

From the word description of the problem, create a state table and/or state diagram showing what the circuit must do. These form the basic technical speciﬁcations for the circuit you will be designing.
Choose a binary code for the states, and create a binary-coded version of the state table and/or state diagram. For N states, the code will need log₂ bits. Any code will work, but some codes may lead to simpler combinational logic in the circuit.
Choose a particular type of ﬂip-ﬂop. This choice is often dictated by the components you have on hand.
Add columns to the state table that show the input required to each ﬂip-ﬂop in order to eﬀect each transition that is required.
Simplify the input(s) to each ﬂip-ﬂop. Karnaugh maps or algebraic methods are good tools for the simpliﬁcation process.
Draw the circuit.

Example 5-a ______________________________________________________________________________________________________

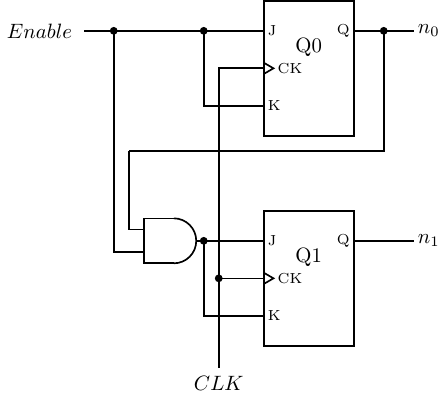
Design a counter that has an Enable input. When Enable = 1 it increments through the sequence 0, 1, 2, 3, 0, 1,…with each clock tick. Enable = 0 causes the counter to remain in its current state.

Solution:

First we create a state table and state diagram:

	Enable = 0	Enable = 1
Current	Next	Next
n	n	n

0	0	1
1	1	2
2	2	3
3	3	0

At each clock tick the counter increments by one if Enable = 1. If Enable = 0 it remains in the current state. We have only shown the inputs because the output is equal to the state.

A reasonable choice is to use the binary numbering system for each state. With four states we need two bits. We will let n = n₁n₀, giving the state table:

		Enable = 0		Enable = 1
Current		Next		Next
n₁	n₀	n₁	n₀	n₁	n₀

0	0	0	0	0	1
0	1	0	1	1	0
1	0	1	0	1	1
1	1	1	1	0	0

Since JK ﬂip-ﬂops are very general we will use those.

We need two ﬂip-ﬂops, one for each bit. So we add columns to the state table showing the input required to each JK ﬂip-ﬂop to cause the correct state transition. Referring to Figure 5.27 (page 402), we see that JK = 00 keeps the current state, JK = 01 resets it (to 0), JK = 10 sets it (to 1), and JK = 11 complements the state. We use X when the input can be either 0 or 1.

		Enable = 0						Enable = 1
Current		Next						Next
n₁	n₀	n₁	n₀	J₁	K₁	J₀	K₀	n₁	n₀	J₁	K₁	J₀	K₀

0	0	0	0	0	X	0	X	0	1	0	X	1	X
0	1	0	1	0	X	X	0	1	0	1	X	X	1
1	0	1	0	X	0	0	X	1	1	X	0	1	X
1	1	1	1	X	0	X	0	0	0	X	1	X	1

Notice the “don’t care” entries in the state table. Since the JK ﬂip-ﬂop is so versatile, including the “don’t cares” helps ﬁnd simpler circuit realizations. (See Exercise 5-3.)

We use Karnaugh maps, using E for Enable.

$\text{[math]}$

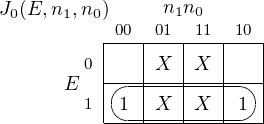
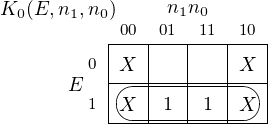
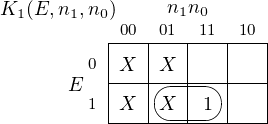
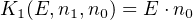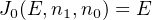$J0(E,n1,n0) = E$

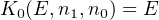$K0(E,n1,n0) = E$

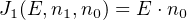$J (E,n ,n ) = E ⋅n 1 1 0 0$

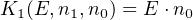$K1 (E, n1,n0) = E ⋅n0$
The circuit to implement this counter is:

The timing of the binary counter is shown here when counting through the sequence 3, 0, 1, 2, 3 (11,00,01,10,11).

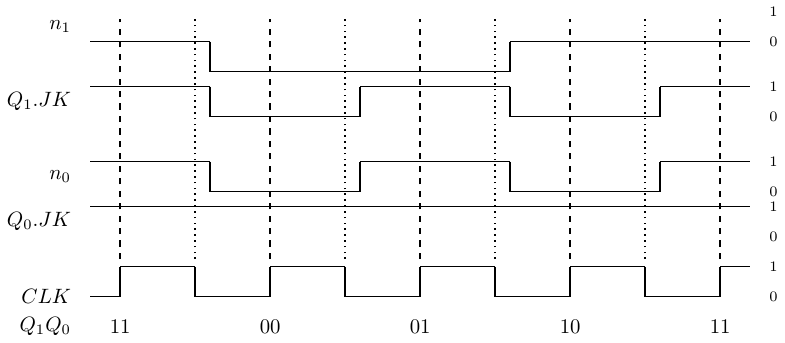
Q_i .JK is the input to the i^th JK ﬂip-ﬂop, and n_i is its output. (Recall that J = K in this design.) When the i^th input, Q_i.JK, is applied to its JK ﬂip-ﬂop, remember that the state of the ﬂip-ﬂop does not change until the second half of the clock cycle. This can be seen when comparing the trace for the corresponding output, n_i, in the ﬁgure.

Note the short delay after a clock transition before the value of each n_i actually changes. This represents the time required for the electronics to completely settle to the new values.

__________________________________________________________________________________□

Except for very inexpensive microcontrollers, most modern CPUs execute instructions in stages. An instruction passes through each stage in an assembly-line fashion, called a pipeline. The action of the ﬁrst stage is to fetch the instruction from memory, as will be explained in Chapter 6.

After an instruction is fetched from memory, it passes onto the next stage. Simultaneously, the ﬁrst stage of the CPU fetches the next instruction from memory. The result is that the CPU is working on several instructions at the same time. This provides some parallelism, thus improving execution speed.

Almost all programs contain conditional branch points — places where the next instruction to be fetched can be in one of two diﬀerent memory locations. Unfortunately, the decision of which of the two instructions to fetch is not known until the decision-making instruction has moved several stages into the pipeline. In order to maintain execution speed, as soon as a conditional branch instruction has passed on from the fetch stage, the CPU needs to predict where to fetch the next instruction from.

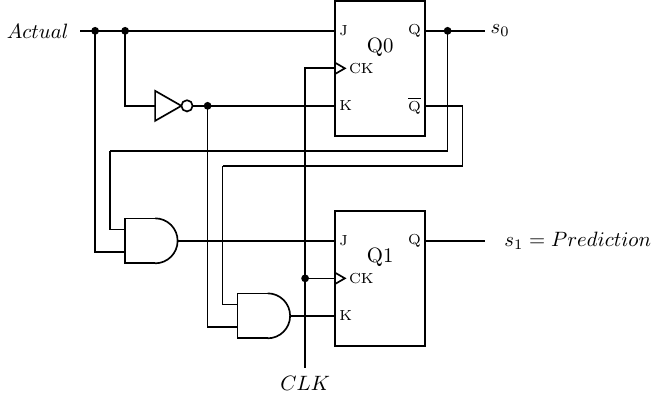
In this next example we will design a circuit to implement a prediction circuit.

Example 5-b ______________________________________________________________________________________________________

Design a circuit that predicts whether a conditional branch is taken or not. The predictor continues to predict the same outcome, take the branch or do not take the branch, until it makes two mistakes in a row.

Solution:

We use “Yes” to indicate when the branch is taken and “No” to indicate when it is not. The state diagram shows four states:

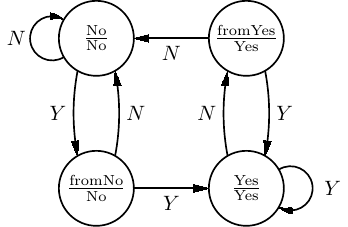
Let us begin in the “No” state. The prediction is that the next branch will also not be taken. The notation in the state bubbles is , showing that the output in this state is also “No.”
The input to the circuit is whether or not the branch was actually taken. The arc labeled “N” shows the transition when the branch was not taken. It loops back to the “No” state, with the prediction (the output) that the branch will not be taken the next time. If the branch is taken, the “Y” arc shows that the circuit moves into the “fromNo” state, but still predicting no branch the next time.
From the “fromNo” state, if the branch is not taken (the prediction is correct), the circuit returns to the “No” state. However, if the branch is taken, the “Y” shows that the circuit moves into the “Yes” state. This means that the circuit predicted incorrectly twice in a row, so the prediction is changed to “Yes.”
You should be able to follow this state diagram for the other cases and convince yourself that both the “fromNo” and “fromYes” states are required.

Next we look at the state table:

		Taken = No		Taken = Y es
Current		Next		Next
State	Prediction	State	Prediction	State	Prediction

No	No	No	No	fromNo	No
fromNo	No	No	No	Y es	Y es
fromY es	Y es	No	No	Y es	Y es
Y es	Y es	fromY es	Y es	Y es	Y es

Since there are four states, we need two bits. We will let 0 represent “No” and 1 represent “Yes.” The input is whether the branch is actually taken (1) or not (0). And the output is the prediction of whether it will be taken (1) or not (0).

We choose a binary code for the state, s₁s₀, such that the high-order bit represents the prediction, and the low-order bit what the last input was. That is:

State	Prediction	s₁	s₀

No	No	0	0
fromNo	No	0	1
fromY es	Y es	1	0
Y es	Y es	1	1

This leads to the state table in binary:

		Input = 0		Input = 1
Current		Next		Next
s₁	s₀	s₁	s₀	s₁	s₀

0	0	0	0	0	1
0	1	0	0	1	1
1	0	0	0	1	1
1	1	1	0	1	1

We will use JK ﬂip-ﬂops for the circuit.

Next we add columns to the binary state table showing the JK inputs required in order to cause the correct state transitions.

		Input = 0						Input = 1
Current		Next						Next
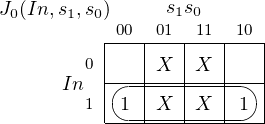
s₁	s₀	s₁	s₀	J₁	K₁	J₀	K₀	s₁	s₀	J₁	K₁	J₀	K₀

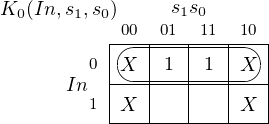
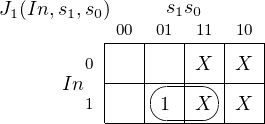
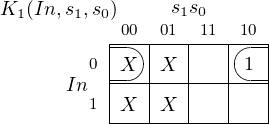
0	0	0	0	0	X	0	X	0	1	0	X	1	X
0	1	0	0	0	X	X	1	1	1	1	X	X	0
1	0	0	0	X	1	0	X	1	1	X	0	1	X
1	1	1	0	X	0	X	1	1	1	X	0	X	0

We use Karnaugh maps to derive equations for the JK ﬂip-ﬂop inputs.

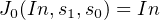$J (In,s ,s ) = In 0 1 0$

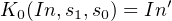$K0 (In,s1,s0) = In′$

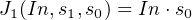$J1(In,s1,s0) = In ⋅s0$

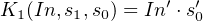$′ ′ K1(In,s1,s0) = In ⋅s0$
The circuit to implement this predictor is:

_____________________________________________________________________________________________________________________________□

5.5 Memory Organization

In this section we will discuss how registers, SRAM, and DRAM are organized and constructed. Keeping with the intent of this book, the discussion will be introductory only.

5.5.1 Registers

Registers are used in places where small amounts of very fast memory is required. Many are found in the CPU where they are used for numerical computations, temporary data storage, etc. They are also used in the hardware that serves to interface between the CPU and other devices in the computer system.

We begin with a simple 4-bit register, which allows us to store four bits. Figure 5.29 shows a design for implementing a 4-bit register using D ﬂip-ﬂops.

Figure 5.29: A 4-bit register. A D ﬂip-ﬂop is used to hold each bit. The state of the i^th bit is set by the value of d_i at each clock tick. The 4-bit value stored in the register is r = r₃r₂r₁r₀.

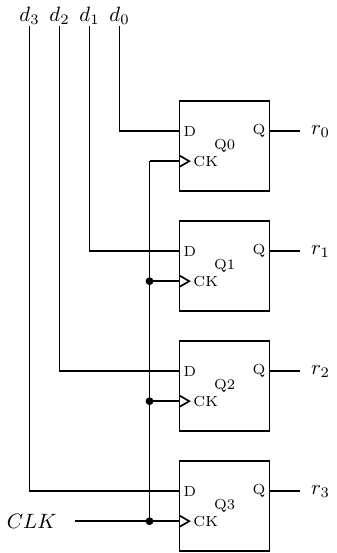
As described above, each time the clock cycles the state of each of the D ﬂip-ﬂops is set according to the value of d = d₃d₂d₁d₀. The problem with this circuit is that any changes in any of the d_is will change the state of the corresponding bit in the next clock cycle, so the contents of the register are essentially valid for only one clock cycle.

One-cycle buﬀering of a bit pattern is suﬃcient for some applications, but there is also a need for registers that will store a value until it is explicitly changed, perhaps billions of clock cycles later. The circuit in Figure 5.30 uses adds a load signal and feedback from the output of each bit. When load = 1 each bit is set according to its corresponding input, d_i. When load = 0 the output of each bit, r_i, is used as the input, giving no change.

Figure 5.30: A 4-bit register with load. The storage portion is the same as in Figure 5.29. When load = 1 each bit is set according to its corresponding input, d_i. When load = 0 the output of each bit, r_i, is used as the input, giving no change.

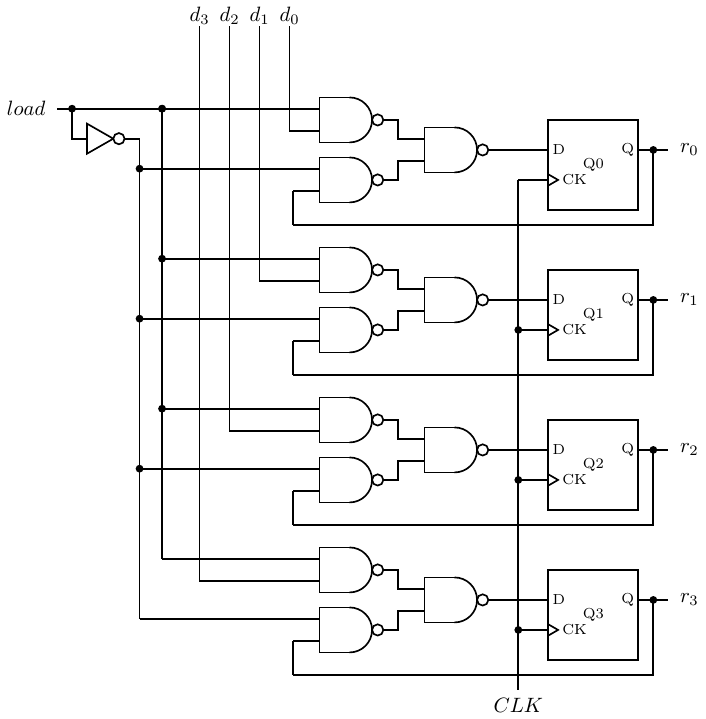
So this register can be used to store a value for as many clock cycles as desired. The value will not be changed until load is set to 1.

Most computers need many general purpose registers. When two or more registers are grouped together, the unit is called a register ﬁle. A mechanism must be provided for addressing one of the registers in the register ﬁle.

Consider a register ﬁle composed of eight 4-bit registers, r0 – r7. We could build eight copies of the circuit shown in Figure 5.30. Let the 4-bit data input, d, be connected in parallel to all of the corresponding data pins, d₃d₂d₁d₀, of each of the eight registers. Three bits are required to address one of the registers (2³ = 8). If the 8-bit output from a 3 × 8 decoder is connected to the eight load inputs of each of the registers, d will be loaded into one, and only one, of the registers during the next clock cycle. All the other registers will have load = 0, and they will simply maintain their current state. Selecting the output from one of the eight registers can be done with four 8-input multiplexers. One such multiplexer is shown in Figure 5.31. The inputs r0_i – r7_i are the i^th bits from each of eight registers, r0 – r7.

Figure 5.31: 8-way mux to select output of register ﬁle. This only shows the output of the i^th bit. n are required for n-bit registers. Reg_Sel is a 3-bit signal that selects one of the eight inputs.

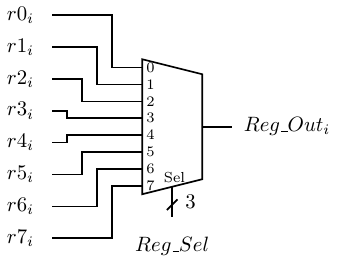
One of the eight registers is selected for the 1-bit output, Reg_Out_i, by the 3-bit input Reg_Sel. Keep in mind that four of these output circuits would be required for 4-bit registers. The same Reg_Sel would be applied to all four multiplexers simultaneously in order to output all four bits of the same register. Larger registers would, of course, require correspondingly more multiplexers.

There is another important feature of this design that follows from the master/slave property of the D ﬂip-ﬂops. The state of the slave portion does not change until the second half of the clock cycle. So the circuit connected to the output of this register can read the current state during the ﬁrst half of the clock cycle, while the master portion is preparing to change the state to the new contents.

5.5.2 Shift Registers

There are many situations where it is desirable to shift a group of bits. A shift register is a common device for doing this. Common applications include:

Inserting a time delay in a bit stream.
Converting a serial bit stream to a parallel group of bits.
Converting a parallel group of bits into a serial bit stream.
Shifting a parallel group of bits left or right to perform multiplication or division by powers of 2.

Serial-to-parallel and parallel-to-serial conversion is required in I/O controllers because most I/O communication is serial bit streams, while data processing in the CPU is performed on groups of bits in parallel.

A simple 4-bit serial-to-parallel shift register is shown in Figure 5.32.

Figure 5.32: Four-bit serial-to-parallel shift register. A D ﬂip-ﬂop is used to hold each bit. Bits arrive at the input, s_i, one at a time. The last four input bits are available in parallel at r₃ – r₀.

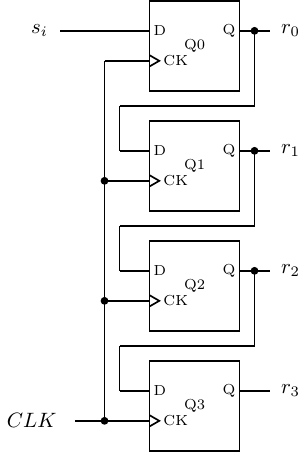
A serial stream of bits is input at s_i. At each clock tick, the output of Q₀ is applied to the input of Q₁, thus copying the previous value of r₀ to the new r₁. The state of Q₀ changes to the value of the new s_i, thus copying this to be the new value of r₀. The serial stream of bits continues to ripple through the four bits of the shift register. At any time, the last four bits in the serial stream are available in parallel at the four outputs, r₃,…,r₀.

The same circuit could be used to provide a time delay of four clock ticks in a serial bit stream. Simply use r₃ as the serial output.

5.5.3 Static Random Access Memory (SRAM)

There are several problems with trying to extend this design to large memory systems. First, although a multiplexer works for selecting the output from several registers, one that selects from a many million memory cells is simply too large. From Figure 5.9 (page 333), we see that such a multiplexer would need an AND gate for each memory cell, plus an OR gate with an input for each of these millions of AND gate outputs.

We need another logic element called a tri-state buﬀer. The tri-state buﬀer has three possible outputs — 0, 1, and “high Z.” “High Z” describes a very high impedance connection (see Section 4.4.2, page 237.) It can be thought of as essentially “no connection” or “open.”

It takes two inputs — data input and enable. The truth table describing a tri-state buﬀer is:

Enable	In	Out

0	0	highZ
0	1	highZ
1	0	0
1	1	1

and its circuit symbol is shown in Figure 5.33.

Figure 5.33: Tri-state buﬀer.

When Enable = 1 the output, which is equal to the input, is connected to whatever circuit element follows the tri-state buﬀer. But when Enable = 0, the output is essentially disconnected. Be careful to realize that this is diﬀerent from 0; being disconnected means it has no eﬀect on the circuit element to which it is connected.

A 4-way multiplexer using a 2 × 4 decoder and four tri-state buﬀers is illustrated in Figure 5.34.

Figure 5.34: Four way multiplexer built from tri-state buﬀers. Output = w, x, y, or z, depending on which one is selected by s₁s₀ fed into the decoder. Compare with Figure 5.9, page 333.

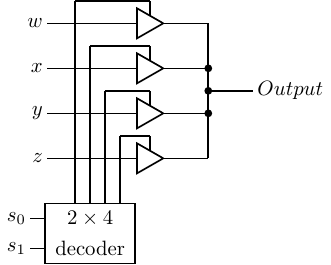
Compare this design with the 4-way multiplexer shown in Figure 5.9, page 333. The tri-state buﬀer design may not be an advantage for small multiplexers. But an n-way multiplexer without tri-state buﬀers requires an n-input OR gate, which presents some technical electronic problems.

Figure 5.35 shows how tri-state buﬀers can be used to implement a single memory cell.

Figure 5.35: 4-bit memory cell. Each bit is output through a tri-state buﬀer. addr_j is one output from a decoder corresponding to an address.

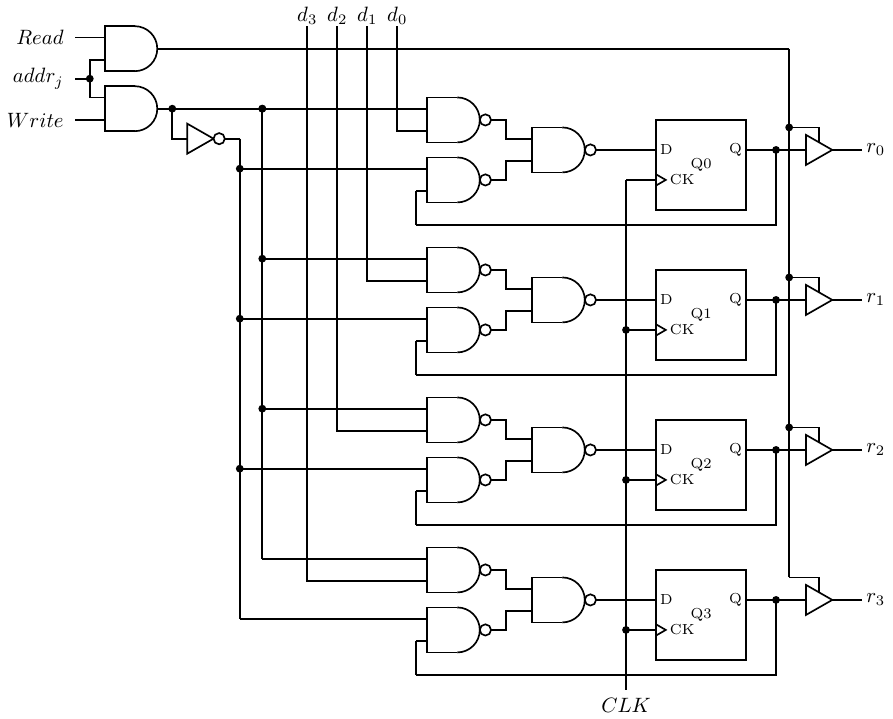
This circuit shows only one 4-bit memory cell so you can compare it with the register design in Figure 5.29, but it scales to much larger memories. Write is asserted to store data in the D ﬂip-ﬂops. Read enables the output tri-state buﬀer in order to connect the single output line to Mem_data_out. The address decoder is also used to enable the tri-state buﬀers to connect a memory cell to the output, r₃r₂r₁r₀.

This type of memory is called Static Random Access Memory (SRAM). “Static” because the memory retains its stored values as long as power to the circuit is maintained. “Random access” because it takes the same length of time to access the memory at any address.

A 1 MB memory requires a 20 bit address. This requires a 20 × 2²⁰ address decoder as shown in Figure 5.36.

Figure 5.36: Addressing 1 MB of memory with one 20×2²⁰ address decoder. The short line through the connector lines indicates the number of bits traveling in parallel in that connection.

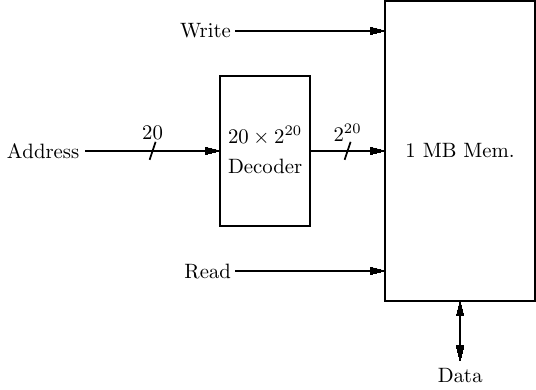
Recall from Section 5.1.3 (page 318) that an n × 2ⁿ decoder requires 2ⁿ AND gates. We can simplify the circuitry by organizing memory into a grid of rows and columns as shown in Figure 5.37.

Figure 5.37: Addressing 1 MB of memory with two 10 × 2¹⁰ address decoders.

Although two decoders are required, each requires 2^n∕2 AND gates, for a total of 2 × 2^n∕2 = 2^(n∕2)+1 AND gates for the decoders. Of course, memory cell access is slightly more complex, and some complexity is added in order to split the 20-bit address into two 10-bit portions.

5.5.4 Dynamic Random Access Memory (DRAM)

Each bit in SRAM requires about six transistors for its implementation. A less expensive solution is found in Dynamic Random Access Memory (DRAM). In DRAM each bit value is stored by a charging a capacitor to one of two voltages. The circuit requires only one transistor to charge the capacitor, as shown in Figure 5.38.

Figure 5.38: Bit storage in DRAM.

This Figure shows only four bits in a single row.

When the “Row Address Select” line is asserted all the transistors in that row are turned on, thus connecting the respective capacitor to the Data Latch. The value stored in the capacitor, high voltage or low voltage, is stored in the Data Latch. There, it is available to be read from the memory. Since this action tends to discharge the capacitors, they must be refreshed from the values stored in the Data Latch.

When new data is to be stored in DRAM, the current values are ﬁrst stored in the Data Latch, just as in a read operation. Then the appropriate changes are made in the Data Latch before the capacitors are refreshed.

These operations take more time than simply switching ﬂip-ﬂops, so DRAM is appreciably slower than SRAM. In addition, capacitors lose their charge over time. So each row of capacitors must be read and refreshed in the order of every 60 msec. This requires additional circuitry and further slows memory access. But the much lower cost of DRAM compared to SRAM warrants the slower access time.

This has been only an introduction to how switching transistors can be connected into circuits to create a CPU. We leave the details to more advanced books, e.g., [20], [23], [24], [28], [31], [34].

5.6 Exercises

The greatest beneﬁt will be derived from these exercises if you either build the circuits with hardware or using a simulation program. Several free circuit simulation applications are available that run under GNU/Linux.

5-1: (§5.1) Build a four-bit adder.
5-2: (§5.1) Build a four-bit adder/subtracter.
5-3: (§5.4) Redesign the 2-bit counter of Example 5-a using only the “set” and “reset” inputs of the JK ﬂip-ﬂops. So your state table will not have any “don’t cares.”
5-4: (§5.4) Design a 4-bit up counter — 0, 1, 2,…,15, 0,…
5-5: (§5.4) Design a 4-bit down counter — 15, 14, 13,…,0, 15,…
5-6: (§5.4) Design a decimal counter — 0, 1, 2,…,9, 0,…
5-7: (§5.5) Build the register ﬁle described in Section 5.5.1. It has eight 4-bit registers. A 3 × 8 decoder is used to select a register to be loaded. Four 8-way multiplexers are used to select the four bits from one register to be output.

[next] [prev] [prev-tail] [front] [up]

Chapter 5Logic Circuits

5.1 Combinational Logic Circuits

5.1.1 Adder Circuits

5.1.2 Ripple-Carry Addition/Subtraction Circuits

5.1.3 Decoders

5.1.4 Multiplexers

5.2 Programmable Logic Devices

5.2.1 Programmable Logic Array (PLA)

5.2.2 Read Only Memory (ROM)

5.2.3 Programmable Array Logic (PAL)

5.3 Sequential Logic Circuits

5.3.1 Clock Pulses

5.3.2 Latches

5.3.3 Flip-Flops

5.4 Designing Sequential Circuits

5.5 Memory Organization

5.5.1 Registers

5.5.2 Shift Registers

5.5.3 Static Random Access Memory (SRAM)

5.5.4 Dynamic Random Access Memory (DRAM)

5.6 Exercises

Chapter 5
Logic Circuits