2 Data Storage Formats

Chapter 2
Data Storage Formats

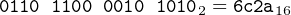
In this chapter, we begin exploring how data is encoded for storage in memory and write some programs in C to explore these concepts. One way to look at a modern computer is that it is made up of:

Billions of two-state switches. Each of the switches is always in one state or the other, and it stays in that state until the control unit changes its state or the power is turned oﬀ.
A control unit that can:
- Detect the state of each switch.
- Change the state of that switch and/or other switches.

There is also provision for communicating with the world outside the computer — input and output.

2.1 Bits and Groups of Bits

Since nearly everything that takes place in a computer, from the instructions that make up a program to the data these instructions act upon, depends upon two-state switches, we need a good notation to use when talking about the states of the switches. It is clearly very cumbersome to say something like,

“The ﬁrst switch is on, the second one is also on,
but the third is oﬀ, while the fourth is on.”

We need a more concise notation, which leads us to use numbers. When dealing with numbers, you are most familiar with the decimal system, which is based on ten, and thus uses ten digits.

Decimal digits:: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Two number systems are useful when talking about the states of switches — the binary system, which is based on two,

Binary digits:: 0, 1

and the hexadecimal system, which is based on sixteen.

Hexadecimal digits:: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f

A less commonly used number system is octal, which is based on eight.

Octal digits:: 0, 1, 2, 3, 4, 5, 6, 7

“Binary digit” is commonly shortened to “bit.” It is common to bypass the fact that a bit represents the state of a switch, and simply call the switches “bits.” Using bits (binary digits), we can greatly simplify the previous statement about switches as 1101, which you can think of as representing “on, on, oﬀ, on.” It does not matter whether we use 1 to represent “on” and 0 as “oﬀ,” or 0 as “on” and 1 as “oﬀ.” We simply need to be consistent. You will see that this will occur naturally; it will not be an issue.

Hexadecimal is commonly used as a shorthand notation to specify bit patterns. Since there are sixteen hexadecimal digits, each one can be used to specify uniquely a group of four bits. Table 2.1 shows the correspondence between each possible group of four bits and one hexadecimal digit. Thus, the above English statement specifying the state of four switches can be written with a single hexadecimal digit, d.

Four binary digits (bits)	One hexadecimal digit
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	a
1011	b
1100	c
1101	d
1110	e
1111	f

Table 2.1: Hexadecimal representation of four bits.

When it is not clear from the context, we will indicate the base of a number in this text with a subscript. For example, 100₁₀ is written in decimal, 100₁₆ is written in hexadecimal, and 100₂ is written in binary.

Hexadecimal digits are especially convenient when we need to specify the state of a group of, say, 16 or 32 switches. In place of each group of four bits, we can write one hexadecimal digit. For example,

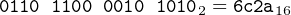0110 1100 0010 10102 = 6c2a16

(2.1)

and

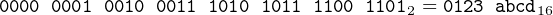0000 0001 0010 0011 1010 1011 1100 11012 = 0123 abcd16

(2.2)

A single bit has limited usefulness when we want to store data. We usually need to use a group of bits to store a data item. This grouping of bits is so common that most modern computers only allow a program to access bits in groups of eight. Each of these groups is called a byte.

byte:: A contiguous group of bits, usually eight.

Historically, the number of bits in a byte has varied depending on the hardware and the operating system. For example, the CDC 6000 series of scientiﬁc mainframe computers used a six-bit byte. Nearly everyone uses “byte” to mean eight bits today.

Another important reason to learn hexadecimal is that the programming language may not allow you to specify a value in binary. Preﬁxing a number with 0x (zero, lower-case ex) in C/C++ means that the number is expressed in hexadecimal. There is no C/C++ syntax for writing a number in binary. The syntax for specifying bit patterns in C/C++ is shown in Table 2.2. (The 32-bit pattern for the decimal value 123 will become clear after you read Sections 2.2 and 2.3.) Although the GNU assembler, as, includes a notation for specifying bit patterns in binary, it is usually more convenient to use the C/C++ notation.

	Preﬁx	Example	32-bit pattern (binary)
Decimal:	none	123	0000 0000 0000 0000 0000 0000 0111 1011
Hexadecimal:	0x	0x123	0000 0000 0000 0000 0000 0001 0010 0011
Octal:	0	0123	00 000 000 000 000 000 000 000 001 010 011

Table 2.2: C/C++ syntax for specifying literal numbers. Octal bits grouped by three for readability.

2.2 Mathematical Equivalence of Binary and Decimal

We have seen in the previous section that binary digits are the natural way to show the states of switches within the computer and that hexadecimal is a convenient way to show the states of up to four switches with only one character. Now we explore some of the mathematical properties of the binary number system and show that it is numerically equivalent to the more familiar decimal (base 10) number system. Showing the mathematical equivalence of the hexadecimal and decimal number systems is left as exercises at the end of this chapter.

We will consider only integers at this point. The mathematical presentation here does, of course, generalize to fractional values. Simply continue the exponents of the radix, r, on to negative values, i.e., n-1, n-2, …, 1, 0, -1, -2, …. This will be covered in detail in Chapter 14.

By convention, we use a positional notation when writing numbers. For example, in the decimal number system, the integer 123 is taken to mean

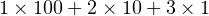1 × 100+ 2× 10 +3 × 1

(2.3)

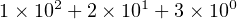1 ×102 + 2× 101 + 3× 100

(2.4)

The right-most digit (3 in Equation2.4) is the least signiﬁcant digit because it “counts” the least in the total value of this number. The left-most digit (1 in this example) is the most signiﬁcant digit because it “counts” the most in the total value of this number.

The base or radix of the decimal number system is ten. There are ten symbols for representing the digits: 0, 1, …, 9. Moving a digit one place to the left increases its value by a factor of ten, and moving it one place to the right decreases its value by a factor of ten. The positional notation generalizes to any radix, r:

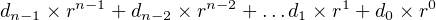dn−1 × rn−1 + dn−2 × rn− 2 + ...d1 ×r1 + d0 × r0

(2.5)

where there are n digits in the number and each d_i = 0, 1, …, r-1. The radix in the binary number system is 2, so there are only two symbols for representing the digits: d_i = 0, 1. We can specialize Equation 2.5 for the binary number system as

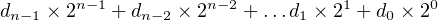n−1 n− 2 1 0 dn−1 × 2 + dn−2 ×2 + ...d1 ×2 + d0 × 2

(2.6)

where there are n digits in the number and each d_i = 0, 1.

For example, the eight-digit binary number 1010 0101 is interpreted as

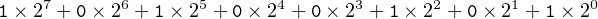1× 27 + 0 × 26 + 1× 25 + 0 × 24 + 0× 23 + 1 × 22 + 0× 21 + 1 ×20

(2.7)

If we evaluate this expression in decimal, we get

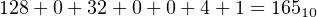128 + 0+ 32+ 0+ 0 + 4+ 1 = 165 10

(2.8)

This example illustrates the method for converting a number from the binary number system to the decimal number system. It is stated in Algorithm 2.1.

Algorithm 2.1: Convert binary to unsigned decimal. (Refer to Equation 2.6.)

1: decimal ← 0
2: for i ← 0,n − 1 do
3: decimal ← decimal + d_i ∗ 2ⁱ
4: end for

Be careful to distinguish the binary number system from writing the state of a bit in binary. Each switch in the computer can be represented by a bit (binary digit), but the entity that it represents may not even be a number, much less a number in the binary number system. For example, the bit pattern 0011 0010 represents the character “2” in the ASCII code for characters. But in the binary number system 0011 0010₂ = 50₁₀.

See Exercises 2-8 and 2-9 for converting hexadecimal to decimal.

2.3 Unsigned Decimal to Binary Conversion

In Section 2.2 (page 23), we covered conversion of a binary number to decimal. In this section we will learn how to convert an unsigned decimal integer to binary. Unsigned numbers have no sign. Signed numbers can be either positive or negative. Say we wish to convert a unsigned decimal integer, N, to binary. We set it equal to the expression in Equation 2.6, giving us:

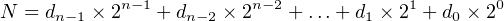N = d × 2n−1 + d × 2n−2 + ...+d × 21 + d × 20 n−1 n−2 1 0

(2.9)

where d_i = 0 or 1. Dividing both sides by 2,

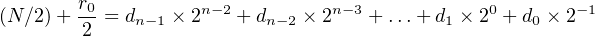(N∕2)+ r0-= dn−1 × 2n−2 + dn−2 × 2n−3 + ...+ d1 × 20 + d0 × 2−1 2

(2.10)

where / is the div operator and the remainder, r₀, is 0 or 1. Since (N∕2) is an integer and all the terms except the 2⁻¹ term on the right-hand side of Equation 2.10 are integers, we can see that d₀ = r₀. Subtracting r₀∕2 from both sides gives,

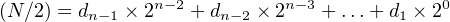(N∕2) = d × 2n−2 + d × 2n−3 + ...+ d × 20 n− 1 n−2 1

(2.11)

Dividing both sides of Equation 2.11 by two:

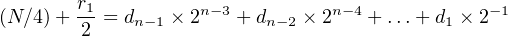(N∕4) + r1= dn−1 ×2n− 3 + dn−2 × 2n−4 + ...+ d1 × 2−1 2

(2.12)

From Equation 2.12 we see that d₁ = r₁. It follows that the binary representation of a number can be produced from right (low-order bit) to left (high-order bit) by applying the algorithm shown in Algorithm 2.2.

Algorithm 2.2: Convert unsigned decimal to binary. (Refer to Equation 2.6.)

1: quotient ← decimal
2: i ← 0
3: d_i ← quotient % 2
4: quotient ← quotient ∕ 2
5: while quotient≠0 do
6: i ← i + 1
7: d_i ← quotient % 2
8: quotient ← quotient ∕ 2
9: end while

Example 2-a ______________________________________________________________________________________________________

Convert 123₁₀ to binary.

Solution:

123 ÷ 2 = 61 + 1∕2	⇒ d₀ = 1
61 ÷ 2 = 30 + 1∕2	⇒ d₁ = 1
30 ÷ 2 = 15 + 0∕2	⇒ d₂ = 0
15 ÷ 2 = 7 + 1∕2	⇒ d₃ = 1
7 ÷ 2 = 3 + 1∕2	⇒ d₄ = 1
3 ÷ 2 = 1 + 1∕2	⇒ d₅ = 1
1 ÷ 2 = 0 + 1∕2	⇒ d₆ = 1
0 ÷ 2 = 0 + 0∕2	⇒ d₇ = 0

123₁₀	= d₇d₆d₅d₄d₃d₂d₁d₀
	= 01111011₂
	= 7b₁₆

__________________________________________________________________________________□

There are times in some programs when it is more natural to specify a bit pattern rather than a decimal number. We have seen that it is possible to easily convert between the number bases, so you could convert the bit pattern to a decimal value, then use that. It is usually much easier to think of the bits in groups of four, then convert the pattern to hexadecimal.

For example, if your algorithm required the use of zeros alternating with ones:

0101 0101 0101 0101 0101 0101 0101 0101

this can be converted to the decimal value

1431655765

or the hexadecimal value (shown here in C/C++ syntax)

0x55555555

Once you have memorized Table 2.1, it is clearly much easier to work with hexadecimal for bit patterns.

The discussion in these two sections has dealt only with unsigned integers. The representation of signed integers depends upon some architectural features of the CPU and will be discussed in Chapter 3 when we discuss computer arithmetic.

2.4 Memory — A Place to Store Data (and Other Things)

We now have the language necessary to begin discussing the major components of a computer. We start with the memory.

You can think of memory as a (very long) array of bytes. Each byte has a particular location (or address) within this array. That is, you could think of

memory[123]

as specifying the 124^th byte in memory. (Don’t forget that array indexing starts with 0.) We generally do not use array notation and simply use the index number, calling it the address or location of the byte.

address (or location):: Identiﬁes a speciﬁc byte in memory.

The address of a particular byte never changes. That is, the 957^th byte from the beginning of memory will always remain the 957^th byte. However, the state of each of the bits — either 0 or 1 — in any given byte can be changed.

Computer scientists typically express the address of each byte in memory in hexadecimal. So we would say that the 957^th byte is at address 0x3bc.

From the discussion of hexadecimal in Section 2.1 (page 15) we can see that the ﬁrst sixteen bytes in memory have the addresses 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, and f. Using the notation

address: contents (bit-pattern-at-the-address)

we show the (possible) contents (the state of the bits) of each of the ﬁrst sixteen bytes of memory in Figure 2.1.

Address	Contents	Address	Contents
00000000:	0110 1010	00000008:	1111 0000
00000001:	1111 0000	00000009:	0000 0010
00000002:	0101 1110	0000000a:	0011 0011
00000003:	0000 0000	0000000b:	0011 1100
00000004:	1111 1111	0000000c:	1100 0011
00000005:	0101 0001	0000000d:	0011 1100
00000006:	1100 1111	0000000e:	0101 0101
00000007:	0001 1000	0000000f:	1010 1010

Figure 2.1: Possible contents of the ﬁrst sixteen bytes of memory; addresses shown in hexadecimal, contents shown in binary. Note that the addresses are shown as 32-bit values. (The contents shown here are arbitrary.)

The state of each bit is indicated by a binary digit (bit) and is arbitrary in Figure 2.1. The bits have been grouped by four for readability. The grouping of the memory bits also shows that we can use two hexadecimal digits to indicate the state of the bits in each byte, as shown in Figure 2.2. For example, the contents of memory location 0000000b are 3c. That means the eight bits that make up the twelfth byte in memory are set to the bit pattern 0011 1100.

Address	Contents	Address	Contents
00000000:	6a	00000008:	f0
00000001:	f0	00000009:	02
00000002:	5e	0000000a:	33
00000003:	00	0000000b:	3c
00000004:	ff	0000000c:	c3
00000005:	51	0000000d:	3c
00000006:	cf	0000000e:	55
00000007:	18	0000000f:	aa

Figure 2.2: Repeat of Figure 2.1 with contents shown in hex. Two hexadecimal characters are required to specify one byte.

Once a bit (switch) in memory is set to either zero or one, it stays in that state until the control unit actively changes it or the power is turned oﬀ. There is an exception. Computers also contain memory in which the bits are permanently set. Such memory is called Read Only Memory or ROM.

Read Only Memory (ROM): : Each bit is permanently set to either zero or one. The control unit can read the state of each bit but cannot change it.

You have probably heard the term “RAM” used for memory that can be changed by the control unit. RAM stands for Random Access Memory. The terminology used here is inconsistent. “Random access” means that it takes the same amount of time to access any byte in the memory. This is in contrast to memory that is sequentially accessible, e.g., tape. The length of time it takes to access a byte on tape depends upon the physical location of the byte with respect to the current tape position.

Random Access Memory (RAM): : The control unit can read the state of each bit and can change it.

A bit can be used to store data. For example, we could use a single bit to indicate whether a student passes a course or not. We might use 0 for “not passed” and 1 for “passed.” A single bit allows only two possible values of a data item. We cannot for example, use a single bit to store a course letter grade — A, B, C, D, or F.

How many bits would we need to store a letter grade? Consider all possible combinations of two bits:

Since there are only four possible bit combinations, we cannot represent all ﬁve letter grades with only two bits. Let’s add another bit and look at all possible bit combinations:

000
001
010
011
100
101
110
111

There are eight possible bit patterns, which is more than suﬃcient to store any one of the ﬁve letter grades. For example, we may choose to use the code

Letter Grade	Bit Pattern
A	000
B	001
C	010
D	011
F	100

This example illustrates two issues that a programmer must consider when storing data in memory in addition to its location(s):

How many bits are required to store the data?: In order to answer this we need to know how many diﬀerent values are allowed for the particular data item. Study the two examples above — two bits and three bits — and you can see that adding a bit doubles the number of possible values. Also, notice that we might not use all the possible bit patterns.
What is the code for storing the data?: Most of the data we deal with in everyday life is not expressed in terms of zeros and ones. In order to store it in computer memory, the programmer must decide upon a code of zeros and ones to use. In the above (three bit) example we used 000 to represent a letter grade of A, 001 to represent B, etc.

Thus, in the grade example, a programmer may choose to store the letter grade at byte number bffffed0 in memory. If the grade is “A”, the programmer would set the bit pattern at location bffffed0 to 00₁₆. If the grade is “C”, the programmer would set the bit pattern at location bffffed0 to 02₁₆. In this example, one of the jobs of an assembly language programmer would be to determine how to set the bit pattern at byte number bffffed0 to the appropriate bit pattern.

High-level languages use data types to determine the number of bits and the storage code. For example, in C you may choose to store the letter grades in the above example in a char variable and use the characters ’A’, ’B’,…,’F’ to indicate the grade. In Section 2.7 you will learn that the compiler would use the following storage formats:

Letter Grade	Bit Pattern
A	0100 0001
B	0100 0010
C	0100 0011
D	0100 0100
F	0100 0101

And programming languages, even assembly language, allow programmers to create symbolic names for memory addresses. The compiler (or assembler) determines the correspondence between the programmer’s symbolic name and the numerical address. The programmer can refer to the address by simply using the symbolic name.

2.5 Using C Programs to Explore Data Formats

Before writing any programs, I urge you to read Appendix B on writing Makeﬁles, even if you are familiar with them. Many of the problems I have helped students solve are due to errors in their Makeﬁle. And many of the Makeﬁle errors go undetected due to the default behavior of the make program.

We will use the C programming language to illustrate these concepts because it takes care of the memory allocation problem, yet still allows us to get reasonably close to the hardware. You probably learned to program in the higher-level, object-oriented paradigm using either C++ or Java. C does not support the object-oriented paradigm.

C is a procedural programming language. The program is divided into functions. Since there are no classes in C, there is no such thing as a member function. The programmer focuses on the algorithms used in each function, and all data items are explicitly passed to the functions.

We can see how this works by exploring the C Standard Library functions, printf and scanf, which are used to write to the screen and read from the keyboard. We will develop a program in C using printf and scanf to illustrate the concepts discussed in the previous sections. The header ﬁle required by either of these functions is:

#include <stdio.h>

which includes the prototype statements for the printf and scanf functions:

int printf(const char *format, ...);
int scanf(const char *format, ...);

printf is used to display text on the screen. The ﬁrst argument, format, controls the text display. At its simplest, format is simply an explicit text string in double quotes.¹ For example,

printf("Hello, world.\n");

would display

Hello, world.

If there are additional arguments, the format string must specify how each of these arguments is to be converted for display. This is accomplished by inserting a conversion code within the format string at the point where the argument value is to be displayed. Each conversion code is introduced by the ’%’ character. For example, Listing 2.1 shows how to display both an int variable and a float variable.

1/*
2 * intAndFloat.c
3 * Using printf to display an integer and a float.
4 * Bob Plantz - 4 June 2009
5 */
6#include <stdio.h>
7
8int main(void)
9{
10    int anInt = 19088743;
11    float aFloat = 19088.743;
12
13    printf("The integer is %i and the float is %f\n", anInt, aFloat);
14
15    return 0;
16}

Listing 2.1: Using printf to display numbers.

Compiling and running the program in Listing 2.1 on my computer gave (user input is boldface):

bob$ gcc -Wall -o intAndFloat intAndFloat.c
bob$ ./intAndFloat
The integer is 19088743 and the float is 19088.742188
bob$

Yes, the float really is that far oﬀ. This will be explained in Chapter 14.

This is not a book about how to use the GNU development environment, so I usually do not show the compile command. I am showing it here to help get you started. You should use the man gcc command to learn about the command line options.

Some common conversion codes are d or i for integer, f for ﬂoat, and x for hexadecimal. The conversion codes may include other characters to specify properties like the ﬁeld width of the display, whether the value is left or right justiﬁed within the ﬁeld, etc. We will not cover the details here. You should read man page 3 for printf to learn more.

scanf is used to read from the keyboard. The format string typically includes only conversion codes that specify how to convert each value as it is entered from the keyboard and stored in the following arguments. Since the values will be stored in variables, it is necessary to pass the address of the variable to scanf. For example, we can store keyboard-entered values in x (an int variable) and y (a float variable) thusly

scanf("%i %f", &x, &y);

The use of printf and scanf are illustrated in the C program in Listing 2.2, which will allow us to explore the mathematical equivalence of the decimal and hexadecimal number systems.

1/*
2 * echoDecHex.c
3 * Asks user to enter a number in decimal and one
4 * in hexadecimal then echoes both in both bases
5 * Bob Plantz - 4 June 2009
6 */
7
8#include <stdio.h>
9
10int main(void)
11{
12    int x;
13    unsigned int y;
14
15    while(1)
16    {
17        printf("Enter a decimal integer (0 to quit): ");
18        scanf("%i", &x);
19        if (x == 0) break;
20
21        printf("Enter a bit pattern in hexadecimal (0 to quit): ");
22        scanf("%x", &y);
23        if (y == 0) break;
24
25        printf("%i is stored as %#010x, and\n", x, x);
26        printf("%#010x represents the decimal integer %i\n\n", y, y);
27    }
28
29    printf("End of program.\n");
30
31    return 0;
32}

Listing 2.2: C program showing the mathematical equivalence of the decimal and hexadecimal number systems.

Here is an example run of this program (user input is boldface):

bob$ ./echoDecHex
Enter a decimal integer: 123
Enter a bit pattern in hexadecimal: 7b
123 is stored as 0x0000007b, and
0x0000007b represents the decimal integer 123

Enter a decimal integer: 0
End of program.
bob$

Let us walk through the program in Listing 2.2.

The program declares two ints, x and y.
The user is prompted to enter an integer in decimal, and the user’s response is read from the keyboard and stored in the memory allocated for x. The conversion code text string passed to scanf, “%i”, causes scanf to interpret the user’s keystrokes as representing a decimal integer. Note that the address of x, &x, must be passed to scanf so that it can store the integer at the memory location named x.
The program next prompts the user to enter a bit pattern in hexadecimal. In this case the conversion code text string passed to scanf is “%x”, which causes scanf to interpret the user’s keystrokes as representing hexadecimal digits. Note that the address of y, &y, must be passed to scanf so that it can store the integer at the memory location named y.
Now let us examine the two printf function calls that display the results. The “%i” conversion code is straightforward. The value of the corresponding variable is displayed in decimal at that point in the text string.
The “%#010x” conversion factor is more interesting. (If you are at a computer read section 3 of the man page for printf as you follow through this description.) The basic conversion is speciﬁed by the “x” character; it causes the value to be displayed in hexadecimal. The “#” character causes an “alternate form” to be used for the display, which is the C syntax for hexadecimal numbers; that is, the value is prefaced by 0x when it is displayed. The ‘0’ character immediately after the ‘#’ character causes ‘0’ to be used as the ﬁll character. The number “10” causes the display to occupy at least ten characters (the ﬁeld width).
Look carefully at the output from this program above. The bit patterns used to store the data input by the user, shown in hexadecimal, show that the unsigned ints are stored in the binary number system (see Section 2.2, page 23 and Section 2.3, page 28). That is, 123₁₀ is stored as 0000007b₁₆.

The program in Listing 2.2 demonstrates a very important concept — hexadecimal is used as a human convenience for stating bit patterns. A number is not inherently binary, decimal, or hexadecimal. A particular value can be expressed in a precisely equivalent way in each of these three number bases. For that matter, it can be expressed equivalently in any number base.

2.6 Examining Memory With gdb

Now that we have started writing programs, you need to learn how to use the GNU debugger, gdb. It may seem premature at this point. The programs are so simple, they hardly require debugging. Well, it is better to learn how to use the debugger on a simple example than on a complicated program that does not work. In other words, tackle one problem at a time.

There is a better reason for learning how to use gdb now. You will ﬁnd that it is a very valuable tool for learning the material in this book, even when you write bug-free programs.

gdb has a large number of commands, but the following are the ones that will be used in this section:

li lineNumber — lists ten lines of the source code, centered at the speciﬁed line number.
break sourceFilename:lineNumber — sets a breakpoint at the speciﬁed line in the source ﬁle. Control will return to gdb when the line number is encountered.
run — begins execution of a program that has been loaded under control of gdb.
cont — continues execution of a program that has been running.
print expression — evaluate expression and display its value.
printf "format", var1, var2,... — displays the values of the vars, using the format speciﬁed in the format string.²
x/nfs memoryAddress — displays (examine) n values in memory in format f of size s starting at memoryAddress.

We will use the program in Listing 2.1 to see how gdb can be used to explore the concepts in more depth. Here is a screen shot of how I compiled the program then used gdb to control the execution of the program and observe the memory contents. My typing is boldface and the session is annotated in italics. Note that you will probably see diﬀerent addresses if you replicate this example on your own (Exercise 2-27).

bob$ gcc -g -Wall -o intAndFloat intAndFloat.c

The “-g” option is required. It tells the compiler to include debugger information in the executable program.

bob$ gdb ./intAndFloat
GNU gdb (Ubuntu/Linaro 7.4-2012.04-0ubuntu2) 7.4-2012.04
Copyright (C) 2012 Free Software Foundation, Inc.
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.  Type "show copying"
and "show warranty" for details.
This GDB was configured as "x86_64-linux-gnu".
For bug reporting instructions, please see:
<http://bugs.launchpad.net/gdb-linaro/>...
Reading symbols from /home/bob/my_book_working/progs/chap02/intAndFloat...done.
(gdb) li
1 /*
2 * intAndFloat.c
3 * Using printf to display an integer and a float.
4 * Bob Plantz - 4 Jun 2009
5 */
6 #include <stdio.h>
7
8 int main(void)
9 {
10     int anInt = 19088743;
(gdb)
11     float aFloat = 19088.743;
12
13     printf("The integer is %i and the float is %f $∖$ n", anInt, aFloat);
14
15     return 0;
16 }
(gdb)

The li command lists ten lines of source code. The display ends with the (gdb) prompt. Pushing the return key will repeat the previous command, and li is smart enough to display the next (up to) ten lines.

(gdb) br 13
Breakpoint 1 at 0x40050b: file intAndFloat.c, line 13.

I set a breakpoint at line 13. When the program is executing, if it ever gets to this statement, execution will pause before the statement is executed, and control will return to gdb.

(gdb) run
Starting program: /home/bob/intAndFloat

Breakpoint 1, main () at intAndFloat.c:13
13 printf("The integer is %i and the float is %f $∖$ n", anInt, aFloat);

The run command causes the program to start execution from the beginning. When it reaches our breakpoint, control returns to gdb.

(gdb) print anInt
$1 = 19088743
(gdb) print aFloat
$2 = 19088.7422

The print command displays the value currently stored in the named variable. There is a round oﬀ error in the ﬂoat value. As mentioned above, this will be explained in Chapter 14.

(gdb) printf "anInt = %i and aFloat = %f $∖$ n", anInt, aFloat
anInt = 19088743 and aFloat = 19088.742188
(gdb) printf "anInt = %#010x and aFloat = %#010x $∖$ n", anInt, aFloat
and in hex, anInt = 0x01234567 and aFloat = 0x00004a90

The printf command can be used to format the displayed values. The formatting string is essentially the same as for the printf function in the C Standard Library.

Take a moment and convert the hexadecimal values to decimal. The value of anInt is correct, but the value of aFloat is 19088₁₀. The reason for this odd behavior is that the x formatting character in the printf function ﬁrst converts the value to an int, then displays that int in hexadecimal. In C/C++, conversion from float to int truncates the fractional part.

Fortunately, gdb provides another command for examining the contents of memory directly — that is, the actual bit patterns. In order to use this command, we need to determine the actual memory addresses where the anInt and aFloat variables are stored.

(gdb) print &anInt
$3 = (int *) 0x7fffffffe058
(gdb) print &aFloat
$4 = (float *) 0x7fffffffe05c

The address-of operator (&) can be used to print the address of a variable. Notice that the addresses are very large. The system is in 64-bit mode, which uses 64-bit addresses. (gdb does not display leading zeros.)

(gdb) help x
Examine memory: x/FMT ADDRESS.
ADDRESS is an expression for the memory address to examine.
FMT is a repeat count followed by a format letter and a size letter.
Format letters are o(octal), x(hex), d(decimal), u(unsigned decimal),
t(binary), f(float), a(address), i(instruction), c(char) and s(string).
Size letters are b(byte), h(halfword), w(word), g(giant, 8 bytes).
The specified number of objects of the specified size are printed
according to the format.

Defaults for format and size letters are those previously used.
Default count is 1. Default address is following last thing printed
with this command or "print".

The x command is used to examine memory. Its help message is very brief, but it tells you everything you need to know.

(gdb) x/1dw 0x7fffffffe058
0x7fffffffe058: 19088743
(gdb) x/1fw 0x7fffffffe05c
0x7fffffffe05c: 19088.7422

The x command can be used to display the values in their stored data type.

(gdb) x/1xw 0x7fffffffe058
0x7fffffffe058: 0x01234567
(gdb) x/4xb 0x7fffffffe058
0x7fffffffe058: 0x67 0x45 0x23 0x01

The display of the anInt variable in hexadecimal, which is located at memory address 0x7fffffffe058, also looks good. However, when displaying these same four bytes as separate values, the least signiﬁcant byte appears ﬁrst in memory.

Notice that in the multiple byte display, the ﬁrst byte (the one that contains 0x67) is located at the address shown on the left of the row. The next byte in the row is at the subsequent address (0x7fffffffe059). So this row displays each of the bytes stored at the four memory addresses 0x7fffffffe058, 0x7fffffffe059, 0x7fffffffe05a, and 0x7fffffffe05b.

(gdb) x/1fw 0x7fffffffe05c
0x7fffffffe05c:     19088.7422
(gdb) x/1xw 0x7fffffffe05c
0x7fffffffe05c:     0x4695217c
(gdb) x/4xb 0x7fffffffe05c
0x7fffffffe05c:     0x7c    0x21    0x95    0x46

The display of the aFloat variable in hexadecimal simply looks wrong. This is due to the storage format of floats, which is very diﬀerent from ints. It will be explained in Chapter 14.

The byte by byte display of the aFloat variable in hexadecimal also shows that it is stored in little endian order.

(gdb) cont
Continuing.
The integer is 19088743 and the float is 19088.742188
[Inferior 1 (process 3221) exited normally]
(gdb) q
bob$

Finally, I continue to the end of the program. Notice that gdb is still running and I have to quit the gdb program.

This example illustrates a property of the x86 processors. Data is stored in memory with the least signiﬁcant byte in the lowest-numbered address. This is called little endian storage. Look again at the display of the four bytes beginning at 0x7fffffffe058 above. We can rearrange this display to show the bit patterns at each of the four locations:

    7fffffffe058: 67
    7fffffffe059: 45
    7fffffffe05a: 23
    7fffffffe05b: 01

Yet when we look at the entire 32-bit value in hexadecimal the bytes seem to be arranged in the proper order:

7fffffffe058: 01234567

When we examine memory one byte at a time, each byte is displayed in numerically ascending addresses. At ﬁrst glance, the value appears to be stored backwards.

We should note here that many processors, e.g., the PowerPC architecture, use big endian storage. As the name suggests, the most signiﬁcant (“biggest”) byte is stored in the ﬁrst (lowest-numbered) memory address. If we ran the program above on a big endian computer, we would see (assuming the variable is located at the same address):

(gdb) x/1xw 0x7fffffffe058
0x7fffffffe058:     0x01234567
(gdb) x/4xb 0x7fffffffe058            [BIG ENDIAN COMPUTER, NOT OURS!]
0x7fffffffe058:     0x01    0x23    0x45    0x67

Generally, you do not need to worry about endianess in a program. It becomes a concern when data is stored as one data type, then accessed as another.

2.7 ASCII Character Code

Almost all programs perform a great deal of text string manipulation. Text strings are made up of groups of characters. The ﬁrst program you wrote was probably a “Hello world” program. If you wrote it in C, you used a statement like:

printf("Hello world\n");

and in C++:

cout << "Hello world\n";

When translating either of these statements into machine code, the compiler must do two things:

store each of the characters in a location in memory where the control unit can access them, and
generate the machine instructions to write the characters on the screen.

We start by considering how a single character is stored in memory. There are many codes for representing characters, but the most common one is the American Standard Code for Information Interchange — ASCII (pronounced “ask’ e”). It uses seven bits to represent each character. Table 2.3 shows the bit patterns for each character in hexadecimal.

bit		bit		bit		bit
pat.	char	pat.	char	pat.	char	pat.	char
00	NUL (Null)	20	(Space)	40	@	60	‘
01	SOH (Start of Hdng)	21	!	41	A	61	a
02	STX (Start of Text)	22	"	42	B	62	b
03	ETX (End of Text)	23	#	43	C	63	c
04	EOT (End of Transmit)	24	$	44	D	64	d
05	ENQ (Enquiry)	25	%	45	E	65	e
06	ACK (Acknowledge)	26	&	46	F	66	f
07	BEL (Bell)	27	’	47	G	67	g
08	BS (Backspace)	28	(	48	H	68	h
09	HT (Horizontal Tab)	29	)	49	I	69	i
0a	LF (Line Feed)	2a	*	4a	J	6a	j
0b	VT (Vertical Tab)	2b	+	4b	K	6b	k
0c	FF (Form Feed)	2c	,	4c	L	6c	l
0d	CR (Carriage Return)	2d	-	4d	M	6d	m
0e	SO (Shift Out)	2e	.	4e	N	6e	n
0f	SI (Shift In)	2f	/	4f	O	6f	o
10	DLE (Data-Link Escape)	30	0	50	P	70	p
11	DC1 (Device Control 1)	31	1	51	Q	71	q
12	DC2 (Device Control 2)	32	2	52	R	72	r
13	DC3 (Device Control 3)	33	3	53	S	73	s
14	DC4 (Device Control 4)	34	4	54	T	74	t
15	NAK (Negative ACK)	35	5	55	U	75	u
16	SYN (Synchronous idle)	36	6	56	V	76	v
17	ETB (End of Trans. Block)	37	7	57	W	77	w
18	CAN (Cancel)	38	8	58	X	78	x
19	EM (End of Medium)	39	9	59	Y	79	y
1a	SUB (Substitute)	3a	:	5a	Z	7a	z
1b	ESC (Escape)	3b	;	5b	[	7b	{
1c	FS (File Separator)	3c	<	5c	∖	7c	\|
1d	GS (Group Separator)	3d	=	5d	]	7d	}
1e	RS (Record Separator)	3e	>	5e	^	7e	∼
1f	US (Unit Separator)	3f	?	5f	_	7f	DEL (Delete)

Table 2.3: ASCII code for representing characters. The bit patterns (bit pat.) are shown in hexadecimal.

It is not the sort of table that you would memorize. However, you should become familiar with some of its general characteristics. In particular, notice that the numerical characters, ‘0’ …‘9’, are in a contiguous sequence in the code, 0x30 …0x39. The same is true of the lower case alphabetic characters, ‘a’ …‘z’, and of the upper case characters, ‘A’ …‘Z’. Notice that the lower case alphabetic characters are numerically higher than the upper case.

The codes in the left-hand column of Table 2.3 (00 through 1f) deﬁne control characters. The ASCII code was developed in the 1960s for transmitting data from a sender to a receiver. If you read some of names of the control characters, you can imagine how they could be used to control the“dialog” between the sender and receiver. They are generated on a keyboard by holding the control key down while pressing an alphabetic key. For example, ctrl-d generates an EOT (End of Transmission) character.

ASCII codes are usually stored in the rightmost seven bits of an eight-bit byte. The eighth bit (the highest-order bit) is called the parity bit. It can be used for error detection in the following way. The sender and receiver would agree ahead of time whether to use even parity or odd parity. Even parity means that an even number of ones is always transmitted in each characters; odd means that an odd number of ones is transmitted. Before transmitting a character in the ASCII code, the sender would adjust the eighth bit such that the total number of ones matched the even or odd agreement. When the code was received, the receiver would count the ones in each eight-bit byte. If the sum did not match the agreement, the receiver knew that one of the bits in the byte had been received incorrectly. Of course, if two bits had been incorrectly received, the error would pass undetected, but the chances of this double error are remarkably small. Modern communication systems are much more reliable, and parity is seldom used when sending individual bytes.

In some environments the high-order bit is used to provide a code for special characters. A little thought will show you that even all eight bits will not support all languages, e.g., Greek, Russian, Chinese. The Unicode character coding has recently been adopted to support documents that use other characters. Java uses Unicode, and C libraries that support Unicode are also available.

A computer system that uses an ASCII video system (most modern computers) can be programmed to send a byte to the screen. The video system interprets the bit pattern as an ASCII code (from Table 2.3) and displays the corresponding character on the screen.

Getting back to the text string, “Hello world∖n”, the compiler would store this as a constant char array. There must be a way to specify the length of the array. In a C-style string this is accomplished by using the sentinel character NUL at the end of the string. So the compiler must allocate thirteen bytes for this string. An example of how this string is stored in memory is shown in Figure 2.3. Notice that C uses the LF character as a single newline character even though the C syntax requires that the programmer write two characters — ’\n’. The area of memory shown includes the three bytes immediately following the text string.

Address	Contents
4004a1:	48
4004a2:	65
4004a3:	6c
4004a4:	6c
4004a5:	6f
4004a6:	20
4004a7:	77
4004a8:	6f
4004a9:	72
4004aa:	6c
4004ab:	64
4004ac:	0a
4004ad:	00
4004ae:	25
4004af:	73
4004b0:	00

Figure 2.3: A text string stored in memory by a C compiler, including three “garbage” bytes after the string. Values are shown in hexadecimal. A diﬀerent compilation will likely place the string in a diﬀerent memory location.

In Pascal the length of the string is speciﬁed by the ﬁrst byte in the string. It is taken to be an 8-bit unsigned integer. So C-style strings are typically processed by sentinel-controlled loops, and count-controlled string processing loops are more common in Pascal. The C++ string class has additional features, but the actual text string is stored as a C-style text string within the C++ string instance.

2.8 write and read Functions

In Section 2.5 (page 37) we used the printf and scanf functions to convert between C data types and single characters written on the screen or read from the keyboard. In this section, we introduce the two system call functions write and read. We will use the write function to send bytes to the screen and the read function to get bytes from the keyboard.

When these low-level functions are used, it is the programmer’s responsibility to convert between the individual characters and the C/C++ data type storage formats. Although this clearly requires more programming eﬀort, we will use them instead of printf and scanf in order to better illustrate data storage formats.

The C program in Listing 2.3 shows how to display the character ’A’ on the screen. This program allocates one byte of memory as a char variable and names it “aLetter.” This byte is initialized to the bit pattern 41₁₆ (’A’ from Table 2.3). The write function is invoked to display the character on the screen. The arguments to write are:

STDOUT_FILENO is deﬁned in the system header ﬁle, unistd.h.³ It is the GNU/Linux ﬁle descriptor for standard out (usually the screen). GNU/Linux sees all devices as ﬁles. When a program is started the operating system opens a path to standard out and assigns it as ﬁle descriptor number 1.
&aLetter is a memory address. The sequence of one-byte bit patterns starting at this address will be sent to standard out.
1 (one) is the number of bytes that will be sent (to standard out) as a result of this call to write.

The program returns a 0 to the operating system.

1/*
2 * oneChar.c
3 * Writes a single character on the screen.
4 * Bob Plantz - 4 June 2009
5 */
6
7#include <unistd.h>
8
9int main(void)
10{
11    char aLetter = ’A’;
12    write(STDOUT_FILENO, &aLetter, 1);  // STDOUT_FILENO is
13                                        // defined in unistd.h
14    return 0;
15}

Listing 2.3: Displaying a single character using C.

Now let’s consider a program that echoes each character entered from the keyboard. We will allocate a single char variable, read one character into the variable, and then echo the character for the user with a message. The program will repeat this sequence one character at a time until the user hits the return key. The program is shown in Listing 2.4.

1/*
2 * echoChar1.c
3 * Echoes a character entered by the user.
4 * Bob Plantz - 4 June 2009
5 */
6
7#include <unistd.h>
8
9int main(void)
10{
11    char aLetter;
12
13    write(STDOUT_FILENO, "Enter one character: ", 21); // prompt user
14    read(STDIN_FILENO, &aLetter, 1);                   // one character
15    write(STDOUT_FILENO, "You entered: ", 13);         // message
16    write(STDOUT_FILENO, &aLetter, 1);
17
18    return 0;
19}

Listing 2.4: Echoing characters entered from the keyboard.

A run of this program gave:

bob$ ./echoChar1
Enter one character: a
You entered: abob$
bob$

which probably looks like the program is not working correctly to you.

Look more carefully at the program behavior. It illustrates some important issues when using the read function. First, how many keys did the user hit? There were actually two keystrokes, the “a” key and the return key. In fact, the program waits until the user hits the return key. The user could have used the delete key to change the character before hitting the return key.

This shows that keyboard input is line buﬀered. Even though the application program is requesting only one character, the operating system does not honor this request until the user hits the return key, thus entering the entire line. Since the line is buﬀered, the user can edit the line before entering it.

Next, the program correctly echoes the ﬁrst key hit then terminates. Upon program termination the shell prompt, bob$, is displayed. But the return character is still in the input buﬀer, and the shell program reads it. The result is the same as if the user had simply pressed the return key in response to the shell prompt.

Here is another run where I entered three characters before hitting the return key:

bob$ ./echoChar1
Enter one character: abc You entered: abob$ bc
bc 1.06.95
Copyright 1991-1994, 1997, 1998, 2000, 2004, 2006 Free Software Foundation, Inc. This is free software with ABSOLUTELY NO WARRANTY. For details type ‘warranty’.

Again, the program correctly echoes the ﬁrst character, but the two characters bc remain in the input line buﬀer. When echoChar1 terminates the shell program reads the remaining characters from the line buﬀer and interprets them as a command. In this case, bc is a program, so the shell executes that program.

An important point of the program in Listing 2.4 is to illustrate the simplistic behavior of the write and read functions. They work at a very low level. It is your responsibility to design your program to interpret each byte that is written to the screen or read from the keyboard.

2.9 Exercises

2-1

(§2.1) Express the following bit patterns in hexadecimal.

a) 0100 0101 0110 0111 b) 1000 1001 1010 1011 c) 1111 1110 1101 1100 d) 0000 0010 0101 0000

2-2

(§2.1) Express the following bit patterns in binary.

a) 83af b) 9001 c) aaaa d) 5555

2-3

(§2.1) How many bits are represented by each of the following?

a) ffffffff b) 7fff58b7def0 c) 1111₂ d) 1111₁₆ e) 00000000₂ f) 00000000₁₆

2-4

(§2.1) How many hexadecimal digits are required to represent each of the following?

a) eight bits b) thirty-two bits c) sixty-four bits d) ten bits e) twenty bits f) seven bits

2-5

(§2.2) Referring to Equation 2.5, what are the values of r, n and each d_i for the decimal number 29458254? The hexadecimal number 29458254?

2-6

(§2.2) Convert the following 8-bit numbers to decimal by hand:

a) 10101010 b) 01010101 c) 11110000 d) 00001111 e) 10000000 f) 01100011 g) 01111011 h) 11111111

2-7

(§2.2) Convert the following 16-bit numbers to decimal by hand:

a) 1010101111001101 b) 0001001000110100 c) 1111111011011100 d) 0000011111010000 e) 1000000000000000 f) 0000010000000000 g) 1111111111111111 h) 0011000000111001

2-8

(§2.2) In Section 2.2 we developed an algorithm for converting from binary to decimal. Develop a similar algorithm for converting from hexadecimal to decimal. Use your new algorithm to convert the following 8-bit numbers to decimal by hand:

a) a0 b) 50 c) ff d) 89 e) 64 f) 0c g) 11 h) c8

2-9

a) a000 b) ffff c) 0400 d) 1111 e) 8888 f) 0190 g) abcd h) 5555

2-10

(§2.3) Convert the following unsigned, decimal integers to 8-bit hexadecimal representation.

a) 100 b) 123 c) 10 d) 88 e) 255 f) 16 g) 32 h) 128

2-11

(§2.3) Convert the following unsigned, decimal integers to 16-bit hexadecimal representation.

a) 1024 b) 1000 c) 32768 d) 32767 e) 256 f) 65535 g) 2005 h) 43981

2-12

(§2.3) Invent a code that would allow us to store letter grades with plus or minus. That is, the grades A, A- B+, B, B-, …, D, D-, F. How many bits are required for your code?

2-13

(§2.3) We have shown how to write only the ﬁrst sixteen addresses in hexadecimal in Figure 2.1. How would you write the address of the seventeenth byte (byte number sixteen) in hexadecimal? Hint: If we started with zero in the decimal number system we would use a ‘9’ to represent the tenth item. How would you represent the eleventh item in the decimal system?

2-14

(§2.3) Redo the table in Figure 2.2 such that it shows the memory contents in decimal.

2-15

(§2.3) Redo the table in Figure 2.2 such that it shows each of the sixteen bytes containing its byte number. That is, byte number 0 contains zero, number 1 contains one, etc. Show the contents in binary.

2-16

2-17

(§2.4) You want to allocate an area in memory for storing any number between 0 and 4,000,000,000. This memory area will start at location 0x2fffeb96. Give the addresses of each byte of memory that will be required.

2-18

(§2.4) You want to allocate an area in memory for storing an array of 30 bytes. The ﬁrst byte will have the value 0x00 stored in it, the second 0x01, the third 0x02, etc. This memory area will start at location 0x001000. Show what this area of memory looks like.

2-19

(§2.4) In Section 2.4 we invented a binary code for representing letter grades. Referring to that code, express each of the grades as an 8-bit unsigned decimal integer.

2-20

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-6. Note that printf and scanf do not have a conversion for binary. Check the answers in hexadecimal.

2-21

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-7. Note that printf and scanf do not have a conversion for binary. Check the answers in hexadecimal.

2-22

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-8.

2-23

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-9.

2-24

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-10.

2-25

(§2.5) Enter the program in Listing 2.2 and check your answers for Exercise 2-11.

2-26

(§2.5) Modify the program in Listing 2.2 so that it also displays the addresses of the x and y variables. Note that addresses are typically displayed in hexadecimal. How many bytes does the compiler allocate for each of the ints?

2-27

(§2.6) Enter the program in Listing 2.1. Follow through the program with gdb as in the example in Section 2.6. Using the numbers you get, explain where the variables anInt and aFloat are stored in memory and what is stored in each location.

2-28

(§2.7) Write a program in C that creates a display similar to Figure 2.3. Hints: use a char* variable to process the string one character at a time; use %08x to format the display of the address.

2-29

(§2.6) Enter the program in Listing 2.4. Explain why there seems to be an extra prompt in the program. Set breakpoints at both the read statement and at the following write statement. Examine the contents of the aLetter variable before the read and after it. Notice that the behavior of gdb seems very strange when dealing with the read statement. Explain the behavior. Hint: Both gdb and the program you are debugging use the same keyboard for input.

2-30

(§2.8) Modify the program in Listing 2.4 so that it prompts the user to enter an entire line, reads the line, then echoes the entire line. Read only one byte at a time from the keyboard.

2-31

(§2.8) This is similar to Exercise 2-30 except that when the newline character is read from the keyboard (and stored in memory), the program replaces the newline character with a NUL character. The program has now read a line from the keyboard and stored it as a C-style text string. If your algorithm is correct, you will be able to read the text string using the read low-level function and display it with the printf library function thusly (assuming the variable where the string is stored is named theString),

printf("%s\n", theString);

and have only one newline. Notice that this program discards the newline generated when the user hits the return key. This is the same behavior you would see if you used

scanf("\%s", theString);

in C, or

cin >> theString;

in C++ to read the input text from the keyboard.

2-32

(§2.8) Write a C program that prompts the user to enter a line of text on the keyboard then echoes the entire line. The program should continue echoing each line until the user responds to the prompt by not entering any text and hitting the return key. Your program should have two functions, writeStr and readLn, in addition to the main function. The text string itself should be stored in a char array in main. Both functions should operate on NUL-terminated text strings.

writeStr takes one argument, a pointer to the string to be displayed and it returns the number of characters actually displayed. It uses the write system call function to write characters to the screen.
readLn takes two arguments, one that points to the char array where the characters are to be stored and one that speciﬁes the maximum number of characters to store in the char array. Additional keystrokes entered by the user should be read from the OS input buﬀer and discarded. readLn should return the number of characters actually stored in the char array. readLn should not store the newline character (’\n’). It uses the read system call function to read characters from the keyboard.

[next] [prev] [prev-tail] [front] [up]

Chapter 2Data Storage Formats