2: Get character.
3: while more characters do
4: accumulator ← 10 × accumulator
5: tempInt ← 0xf & character
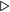 ’&’ is bitwise AND
’&’ is bitwise AND 6: accumulator ← accumulator + tempInt
7: Get character.
8: end while
We saw in Section 3.5 (page 118) that input read from the keyboard and output written on the screen is in the ASCII code and that integers are stored in the binary number system. So if a program reads user input as, say, 12310, that input is read as the characters ’1’, ’2’, and ’3’’, but the value used in the program is represented by the bit pattern 0000007b16.1 In this chapter, we return to the conversion algorithms between these two storage codes and look at the assembly language that is involved.
Two numeric operators, addition and subtraction, were introduced in Section 9.2 (page 607). Many data items are better thought of as bit patterns rather than numerical entities. For example, study Table 2.3 on page 49 and see if you can determine which bit determines the case (upper/lower) of the alphabetic characters.
In order to manipulate individual character codes in a text string, we introduce the bit-wise logical operators in this section. The logical operations are shown in the truth tables in Figure 3.4 (page 134). The instructions available to us to perform these three operations are:
|
| ands | source, destination | |
|
| ors | source, destination | |
|
| xors | source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
|
| and | destination, source | |
| Intel® Syntax |
| or | destination, source |
|
| xor | destination, source | |
For example, the instruction
performs an and operation between each of the respective 32 bits in the eax register with the 32 bits in the edx register, leaving the result in the edx register. The instruction
performs an and operation between each of the respective 8 bits in the dh register with the 8 bits in the ah register, leaving the result in the ah register.
The addressing modes available for the arithmetic operators, add and sub, are also available for the logical operators. For example, if eax contains the bit pattern 0x89abcdef, the instruction
would change eax to contain 0x89abcdee. If we follow this with the instruction
the bit pattern in eax becomes 0x99bbddff. Finally, if we then use
we end up with 0x99bbccee in eax.
The program in Listing 12.1 shows the use of the C bit-wise logical operators “&” and “|” to change the case of alphabetic characters.
The program assumes that the user enters all alphabetic characters without making mistakes. Of course, the conversions could be accomplished with addition and subtraction, but in this application the bit-wise logical operators are more natural.
In Listing 12.2 we show only the gcc-generated assembly language for the main and toUpper functions.
The toLower function is similar to the toUpper, and the writeStr and readLn functions were covered in the exercises in Chapter 11.
Most of the code in Listing 12.2 should be familiar from previous chapters. Note that the C code specifies char arrays in the main function that are 50 elements long (lines 13 and 14). But the compiler generates assembly language that allocates 64 bytes for each array:
and:
Recall that this 16-byte address alignment is specified by the ABI [25].
The code sequence on lines 21 – 23 in main:
is new to you. This code sequence stores a value supplied by the operating system near the end of the stack. The purpose is described in the gcc man page entry for the -fstack-protector option:
Emit extra code to check for buffer overflows, such as stack smashing attacks. This is done by adding a guard variable to functions with vulnerable objects. This includes functions that call alloca, and functions with buffers larger than 8 bytes. The guards are initialized when a function is entered and then checked when the function exits. If a guard check fails, an error message is printed and the program exits.
The value stored there is checked at the end of the function, on lines 54 – 58:
If the value has been overwritten, the __stack_chk_fail function is called, which notifies the user about the problem.
Your version of gcc may be compiled without this option as the default. It can be turned off with the -fno-stack-protector option. Since the assembly language we are writing in this book is not “industrial strength,” we will not include this stack protection code.
In the toUpper function, the compiler-generated assembly language first loads the address stored in the srcPtr variable into a register so it can dereference the pointer.
It then moves the byte at that address into the register, using the movzbl instruction to zero out the remaining 24 bits of the register. (Recall that changing the low-order 32 bits of a register also zeros out the high-order 32 bits.)
Next it moves the byte into another working register and then performs the bit-wise and operation with the bit pattern ffffffdf (= −3310), leaving the result in the edx register. This and operation leaves all the bits in the edx register as they were, except the sixth bit is set to zero. The sixth bit in the ASCII code determines whether a letter is upper or lower case.
Regardless of whether the letter was upper or lower case, it is now upper case. The letter is stored in the low-order eight bits of the edx register, the dl register. So the program loads the address stored in the destPtr variable into a register so it can dereference it and store the character there.
We will now consider the version of this program written in assembly language (Listing 12.3).
Again, we will describe on the toUpper function. Writing directly in assembly language, we also need to get the address in srcPtr so we can dereference it. But in copying the character stored there, we simply ignore the remaining 56 bits of the rax register. Notice that the movb instruction first uses the full 64-bit address in the rax register to fetch the byte stored there, and it then can write over the low-order 8 bits of the same register. (This, of course, “destroys” the address.)
Since we are ignoring the high-order 56 bits of the rax register, we must be consistent when operating on the data in the low-order 8 bits. So we use the andb instruction to operate only on the al portion of the rax register.
Storing the final result is the same, except we are using different registers.
Both ways of implementing this algorithm are correct, and there is probably no significant efficiency difference. However, comparing the two shows the importance of maintaining consistency in data sizes. You do not need to zero out unused portions of registers, but you should also never assume that they are zero.
It is sometimes useful to be able to shift all the bits to the left or right. Since the relative position of a bit in an integer has significance, shifting all the bits to the left one position effectively multiplies the value by two. And shifting them one position to the right effectively divides the value by two. As you will see in Sections 12.3 and 12.4, the multiplication and division instructions are complicated. They also take a great deal of processor time. Using left/right shifts to effect multiplication/division by powers of two is very efficient.
There are two instructions for shifting bits to the right — shift right and shift arithmetic right:
|
| shrs | source, destination | |
|
| sars | source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
|
| shr | destination, source | |
| Intel® Syntax |
| sar | destination, source |
The source operand can be either an immediate value, or the value can be located in the cl register. If it is an immediate value, it can be up to 6310. The destination operand can be either a memory location or a register. Any of the addressing modes that we have covered can be used to specify a memory location.
The action of the shr instruction is to shift all the bits in the destination operand to the right by the number of bit positions specified by the source operand. The “vacated” bit positions at the high-order end of the destination operand are filled with zeros. The last bit to be shifted out of the low-order bit position is copied into the carry flag (CF). For example, if the eax register contained the bit pattern aabb 2233, then the instruction
would produce
and the CF would be one. With the same initial conditions, the instruction
would produce
and the CF would be zero.
The action of the sar instruction is to shift all the bits in the destination operand to the right by the number of bit positions specified by the source operand. The “vacated” bit positions at the high-order end of the destination operand are filled with the same value that was originally in the highest-order bit. The last bit to be shifted out of the low order bit position is copied into the carry flag (CF). For example, if the eax register contained the bit pattern aabb 2233, then the instruction
would produce
and the CF would be one. With the same initial conditions, the instruction
would produce
and the CF would be zero.
Thus the difference between “shift right” and “shift arithmetic right” is that the arithmetic shift preserves the sign of the value – as though it represents an integer stored in two’s complement code.
There are two instructions for shifting bits to the left — shift left and shift arithmetic left:
|
| shls | source, destination | |
|
| sals | source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
|
| shl | destination, source | |
| Intel® Syntax |
| sal | destination, source |
The source operand can be either an immediate value, or the value can be located in the cl register. If it is an immediate value, it can be up to 3110. The destination operand can be either a memory location or a register. Any of the addressing modes that we have covered can be used to specify a memory location.
The action of both the shl and sal instructions is to shift all the bits in the destination operand to the left by the number of bit positions specified by the source operand. In fact, these are really two different assembly language mnemonics for the same machine code. The “vacated” bit positions at the low-order end of the destination operand are filled with zeros. The last bit to be shifted out of the highest-order bit position is copied into the carry flag (CF). For example, if the eax register contained the bit pattern bbaa 2233, then the instruction
would produce
and the CF would be zero. With the same initial conditions, the instruction
would produce
and the CF would be one.
We see how shifts can be used in the hexToInt function shown in Listing 12.4.
Notice that “«” (on line 20 in the hexToInt function) is the left shift operator and “»” is the right shift operator in C/C++. In C++ these operators are overloaded to provide file output and input.
The code in the main function is familiar. The compiler-generated assembly language for hexToInt is shown in Listing 12.5 with comments added.
As usual, gcc has converted the while loop in hexToInt to a do-while loop, which is entered at the bottom. Most of this code has been covered previously. The instruction
shifts the 64 bits that make up the value of the variable accumulator four bits to the left. Make sure that you understand the four high-order bits in this group of 64 are lost. That is, the shift does not carry on to other memory areas beyond these 64 bits. As stated above, the last bit to get shifted out of these 64 bits is copied to the CF.
The conversions from characters to integers
and
start by moving a one-byte character into an int-sized register with the high-order 24 bits zeroed. The actual conversion consists of subtracting off the “character part” as an integer arithmetic operation. Then the result, which is guaranteed to fit within a byte, is stored back in the single byte allocated for the original character.
Actually, we can easily see that the result of this conversion operation is a four-bit value in the range 00002 – 11112. The four-bit left shift of the variable accumulator has left space for inserting these four bits. The bit insertion operation consists of first type casting the four-bit integer to a 64-bit integer as we load it from the variable:
then adding this 64-bit integer to the variable accumulator:
We also note that although the standard return value is 32-bits in the eax register, declaring a long int (64-bit) return value causes the compiler to use the entire rax register:
Listing 12.6 shows a version of the hexToInt function written in assembly language.
It differs from the C version in several ways. First, since this is a leaf function, we do not save the argument in the stack frame. Instead, we simply use the register as the stringPtr variable:
We do, however, explicitly allocate stack space for the local variable:
Although this is not required because this is a leaf function, it is somewhat better software engineering. If this function is ever modified such that it does call another function, the programmer may forget to allocate the stack space, which would then be required. There is less chance that saving the contents of the rdi register would be overlooked since it is the where the first argument is passed. Both of these issues are arguable design decisions.
Next, for the conversion from 4-bit integer values to 64-bit, we define a bit mask:
Performing an and operation with this bit mask leaves the four low-order bits as they were and sets the 60 high-order bits all to zero. Then we simply add this to the 64-bit accumulator (which has already been shifted four bits to the left) it effectively insert the four bits into the correct location:
The hexToInt function discussed in Section 12.2 shows how to convert a string of hexadecimal characters into the integer they represent. That function uses the fact that each hexadecimal character represents four bits. So as the characters are read from left to right, the bits in the accumulator are shifted four places to the left in order to make space for the next four-bit value. The character is converted to the four bits it represents and added to the accumulator.
Although the four-bit left shift seems natural for hexadecimal, it is equivalent to multiplying the value in the accumulator by sixteen. This follows from the positional notation used to write numbers. Add another hexadecimal digit to the right of an existing number effectively multiplies that existing number by sixteen. A little thought shows that this algorithm, shown in Algorithm 12.1, works in any number base.
Of course, you probably want to write programs that allow users to work with decimal numbers. So we need to know how to convert a string of decimal characters to the integer they represent. The characters that represent decimal numbers are in the range 3016 – 3916. Table 12.1 shows the 32-bit int that corresponds to each numeric character.
| Numeral | int |
| (ASCII code) | (Binary number system) |
| 0011 0000 | 0000 0000 0000 0000 0000 0000 0000 0000 |
| 0011 0001 | 0000 0000 0000 0000 0000 0000 0000 0001 |
| 0011 0010 | 0000 0000 0000 0000 0000 0000 0000 0010 |
| 0011 0011 | 0000 0000 0000 0000 0000 0000 0000 0011 |
| 0011 0100 | 0000 0000 0000 0000 0000 0000 0000 0100 |
| 0011 0101 | 0000 0000 0000 0000 0000 0000 0000 0101 |
| 0011 0110 | 0000 0000 0000 0000 0000 0000 0000 0110 |
| 0011 0111 | 0000 0000 0000 0000 0000 0000 0000 0111 |
| 0011 1000 | 0000 0000 0000 0000 0000 0000 0000 1000 |
| 0011 1001 | 0000 0000 0000 0000 0000 0000 0000 1001 |
For a string of characters that represents a decimal integer, Algorithm 12.1 can be specialized to give Algorithm 12.2. (Recall that “⋅” is the bit-wise and operator.)
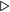 ’&’ is bitwise AND
’&’ is bitwise AND Shifting N bits to the left multiplies a number by 2N, so it can only be used to multiply by powers of two. Algorithm 12.2 multiplies the accumulator by 10, which cannot be accomplished with only shifts. Thus, we need to use the multiplication instruction for decimal conversions.
The multiplication instruction is somewhat more complicated than addition. The main problem is that the product can, in general, occupy the number of digits in the multiplier plus the number of digits in the multiplicand. This is easily seen by computing 99 × 99 = 9801 (in decimal). Thus in general,
| 8-bit × 8-bit | ⇒ 16-bit | ||
| 16-bit × 16-bit | ⇒ 32-bit | ||
| 32-bit × 32-bit | ⇒ 64-bit | ||
| 64-bit × 64-bit | ⇒ 128-bit | ||
The unsigned multiplication instruction is:
|
| muls | source | |
where s denotes the size of the operands:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
| Intel® Syntax |
| mul | source |
In the x86-64 architecture, the destination operand contains the multiplicand and must be in the al, ax, eax, or rax register, depending on the size of the operand, for the unsigned multiplication instruction, mul. This register is not specified as an operand. The instruction specifies the source operand, which contains the multiplier and must be the same size. It can be located in another general-purpose register or in memory. If the numbers are eight bits (hence, one number is in al), the high-order portion of the result will be in the ah register, and the low-order portion of the result will be in the al register. For sixteen and thirty-two bit numbers, the low-order portion of the product will be stored in a portion of the rax register and the high-order will be stored in a portion of the rdx register as shown in Table 12.2.
| Operand | Portion | High-Order | Low-Order |
| Size | of A Reg. | Result | Result |
| 8 bits | al | ah | al |
| 16 bits | ax | dx | ax |
| 32 bits | eax | edx | eax |
| 64 bits | rax | rdx | rax |
For example, let’s see how the computation 7 × 24 = 168 looks in 8-bit, 16-bit, and 32-bit values. First, note that:
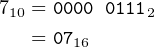 | (12.1) |
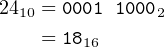 | (12.2) |
and
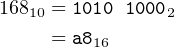 | (12.3) |
Now, if we declare the constants:
These declarations cause the assembler to do the following:
First, consider 8-bit multiplication. If eax contains the bit pattern 0x??????07, then
changes eax such that it contains 0x????00a8. Notice that only the al portion of the A register can be used for the operand, but the result will occupy the entire ax portion of the register even though the result would fit into only the al portion. That is, the instruction will produce a 16-bit result, and anything stored in the ah portion will be lost.
Next, consider 16-bit multiplication. If eax contains 0x????0007, then
changes eax to contain 0x????00a8 and edx to contain 0x????0000. Two points are important in this example:
Finally, 32-bit multiplication. If eax contains 0x00000007, then
changes eax to contain 0x000000a8 and edx to contain 0x00000000. This example shows the entire eax register must be used for the operand before mull is executed, and the entire edx register is used for the high-order portion of the result, even though it is not needed. That is, the instruction will produce a 64-bit result, and anything stored in the edx register will be lost.
These examples show that the rax and rdx registers are used without ever explicitly appearing in the instruction. You must be very careful not to write over a required value that is stored in one of these registers. Using the multiplication instruction requires some careful planning.
There is also a signed multiply instruction, which has three forms:
|
| imuls | source | |
|
| imuls | source, destination | |
|
| imuls | immediate, source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
|
| imul | source | |
| Intel® Syntax |
| imul | destination, source |
|
| imul | destination, source, immediate | |
In the one-operand format the signed multiply instruction uses the rdx:rax register combination in the same way as the mul instruction.
In its two-operand format the destination must be a register. The source can be a register, an immediate value, or a memory location. The source and destination are multiplied, and the result is stored in the destination register. Unfortunately, if the result is too large to fit into the destination register, it is simply truncated. In this case, both the CF and OF flags are set to 1. If the result was able to fit into the destination register, both flags are set to 0.
In its three-operand format the destination must be a register. The source can be a register or a memory location. The source is multiplied by the immediate value and the result is stored in the destination register. As in the two-operand form, if the result is too large to fit into the destination register, it is simply truncated. In this case, both the CF and OF flags are set to 1. If the result was able to fit into the destination register, both flags are set to 0.
The difference between signed and unsigned multiplication can be illustrated with the following multiplication of two 16-bit values. Given the declaration:
and the initial conditions in the rdx and rax registers:
Indeed, starting with the initial conditions above, the instruction:
yields:
yields:
Multiplication is used on line 19 in the decToInt function shown in Listing 12.7.
As we can see on line 17 in Listing 12.8 the compiler has chosen to use the imull instruction for multiplication.
Recall that the destination must be in a register. The compiler has chosen eax in this case. The value to be multiplied must be loaded from its memory location into the register, multiplied, then stored back into memory:
It may appear that the compiler has made an error here. Since both the multiplier and the multiplicand are 32-bit values, the product can be 64 bits wide. However, the compiler has chosen code that assumes the product will be no wider than 32 bits. This can lead to arithmetic errors when multiplying large integers, but according to the C programming language standard [10] this is acceptable:
A computation involving unsigned operands can never overflow, because a result that cannot be represented by the resulting unsigned integer type is reduced modulo the number that is one greater than the largest value that can be represented by the resulting type.
In Listing 12.9 the programmer has chosen unsigned multiplication, mull.
And since this is a leaf function, the register used to pass the address of the text string (rdi) is simply used as the pointer variable rather than allocate a register save area in the stack frame:
This is safe because no other functions are called within this loop. Of course, the programmer must be careful that the pointer variable (rdi) is not changed unintentionally.
Division poses a different problem. In general, the quotient will not be larger than the dividend (except when attempting to divide by zero). Division is also complicated by the existence of a remainder. The divide instruction starts with a dividend that is twice as wide as the divisor. Both the quotient and remainder are the same width as the divisor. The unsigned division instruction is:
|
| divs | source | |
where s denotes the size of the operands:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
| Intel® Syntax |
| div | source |
The source operand specifies the divisor. It can be either a register or a memory location. Table 12.3 shows how to set up the registers with the dividend and where the quotient and remainder will be located after the unsigned division instruction, div, is executed. Notice that the quotient is the C ‘/’ operation, and the remainder is the ‘%’ operation.
| Operand | High-Order | Low-Order | ||
| Size | Dividend | Dividend | Quotient | Remainder |
| 8 bits | ah | al | al | ah |
| 16 bits | dx | ax | ax | dx |
| 32 bits | edx | eax | eax | edx |
| 64 bits | rdx | rax | rax | rdx |
Notice that these instructions do not explicitly specify any operands, but they may change the rax and rdx registers. They do not affect the condition codes in the rflags register.
For example, let’s see how the computation 93 ÷ 19 = 4 with remainder 17 looks in 8-bit, 16-bit, and 32-bit values. First, note that:
| (12.4) |
and
| (12.5) |
Now if we declare the constants:
These declarations cause the assembler to do the following:
First, consider 8-bit division. If eax contains the bit pattern 0x????005d, then
changes eax such that it contains 0x????1104. Notice that ah had to be set to 0 before executing divb even though the dividend fits into one byte. That’s because the divb instruction starts with the ah:al pair as a 16-bit number. We also see that after executing the instruction, ax contains what appears to be a much larger number as a result of the division. Of course, we no longer consider ax, but al (the quotient) and ah (the remainder) as two separate numbers.
Next, consider 16-bit division. If eax contains 0x????005d and edx 0x????0000, then
changes eax to contain 0x????0004 and edx to contain 0x????0011. You may wonder why the divw instruction does not start with the 32-bit dividend in eax. This is for backward compatibility — Intel processors prior to the 80386 had only 16-bit registers.
Finally, 32-bit division. If eax contains 0x0000005d and edx 0x00000000, then
changes eax to contain 0x00000004 and edx to contain 0x00000011. Again, we see that the entire edx register must be filled with zeros before executing the divl instruction, even though the dividend fits within two bytes.
One of the more common errors with division occurs when performing repeated division of a number. Since the first division places the remainder in the area occupied by the high-order portion of the dividend, you must remember to set that area to the appropriate value before dividing again.
The signed division instruction is:
|
| idivs | source | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
| Intel® Syntax |
| idiv | source |
Unlike the signed multiply instruction, signed divide only has one form, which is the same as unsigned divide. That is, the divisor is in the source operand, and the dividend is set up in the rax and rdx registers as shown in Table 12.3.
There is a nice set of instructions that set up the dividend in the rdx and rax registers, using the contents of the rax register, for signed division. These are shown in Table 12.4. The notation dx:ax, edx:eax, and rdx:rax, means that the high-order portion of the doubled, sign extended, value is placed in the respective portion of the rdx register.
| AT&T syntax | Intel® syntax | start | result |
| cbtw | cbw | byte in al | word in ax |
| cwtd | cwd | word in ax | long in dx:ax |
| cltd | cdq | lonq in eax | quad in edx:eax |
| cqto | cqo | quad in rax | octuple in rdx:rax |
We can see the difference between signed and unsigned division by dividing a 32-bit value by a 16-bit value. Given the declaration:
and loading the 32-bit dividend 32768 into the dx:ax register pair (using hexadecimal):
produces the conditions
gives:
With signed integers we need to sign extend when setting up the dx:ax register pair:
which sets up the registers:
When we use the signed divide instruction, we are dividing -32767 (= 800016) by 100. We expect to get -327 with a remainder of -68. Indeed, signed division:
yields:
The “/” operation is used on line 34 in the intToUDec function shown in Listing 12.7, and the “%” operation is used on line 35.
The assembly language generated by gcc is shown in Listing 12.11 (with comments added).
Compare the code sequence from lines 25 – 30:
with that from lines 31 – 36:
Even though the divl instruction produces both the quotient (“/” operation) and remainder (“%” operation), the compiler uses almost the same code sequence twice, once for each operation.
In Listing 12.12 the programmer has chosen to retrieve both the quotient and the remainder from one execution of the divl instruction.
On line 38 the high-order 32 bits of the quotient (edx register) are set to 0.
The division on line 39 leaves “x / base” in the eax register for the next execution of the loop body. It also places “x % base” in the edx register. We know that this value is in the range 0 – 9 and thus fits entirely within the dl portion of the register. Lines 40 and 41 show how the value is converted to its ASCII equivalent and stored in the local char array.
As in the decToUInt function (Listing 12.9), since this is a leaf function, the register used to pass the address of the text string (rdi) is simply used as the pointer variable rather than allocate a register save area in the stack frame. Similarly, the eax register is used as the local “x” variable.
For dealing with signed numbers, the x86-64 architecture provides an instruction that will perform the two’s complement operation. That is, this instruction will negate an integer that is stored in the two’s complement notation. The mnemonic for the instruction is neg.
|
| negs | source | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
| Intel® Syntax |
| neg | source |
neg performs a two’s complement operation on the value in the operand, which can be either a memory location or a register. Any of the addressing modes that we have covered can be used to specify a memory location.
This summary shows the assembly language instructions introduced thus far in the book. The page number where the instruction is explained in more detail, which may be in a subsequent chapter, is also given. This book provides only an introduction to the usage of each instruction. You need to consult the manuals ([2] – [6], [14] – [18]) in order to learn all the possible uses of the instructions.
| data movement: | ||||
| opcode | source | destination | action | page |
| cbtw | convert byte to word, al → ax | 696 | ||
| cwtl | convert word to long, ax → eax | 696 | ||
| cltq | convert long to quad, eax → rax | 696 | ||
| cwtd | convert word to long, ax → dx:ax | 786 | ||
| cltd | convert long to quad, eax → edx:eax | 786 | ||
| cqto | convert quad to octuple, rax → rdx:rax | 786 | ||
| cmovcc | %reg/mem | %reg | conditional move | 706 |
| movs | $imm/%reg | %reg/mem | move | 506 |
| movs | mem | %reg | move | 506 |
| movsss | $imm/%reg | %reg/mem | move, sign extend | 693 |
| movzss | $imm/%reg | %reg/mem | move, zero extend | 693 |
| popw | %reg/mem | pop from stack | 566 | |
| pushw | $imm/%reg/mem | push onto stack | 566 | |
| s = b, w, l, q; w = l, q; cc = condition codes
| ||||
| arithmetic/logic:
| ||||
| opcode | source | destination | action | page |
| adds | $imm/%reg | %reg/mem | add | 607 |
| adds | mem | %reg | add | 607 |
| ands | $imm/%reg | %reg/mem | bit-wise and | 747 |
| ands | mem | %reg | bit-wise and | 747 |
| cmps | $imm/%reg | %reg/mem | compare | 676 |
| cmps | mem | %reg | compare | 676 |
| decs | %reg/mem | decrement | 699 | |
| divs | %reg/mem | unsigned divide | 777 | |
| idivs | %reg/mem | signed divide | 784 | |
| imuls | %reg/mem | signed multiply | 775 | |
| incs | %reg/mem | increment | 698 | |
| leaw | mem | %reg | load effective address | 579 |
| muls | %reg/mem | unsigned multiply | 769 | |
| negs | %reg/mem | negate | 789 | |
| ors | $imm/%reg | %reg/mem | bit-wise inclusive or | 747 |
| ors | mem | %reg | bit-wise inclusive or | 747 |
| sals | $imm/%cl | %reg/mem | shift arithmetic left | 756 |
| sars | $imm/%cl | %reg/mem | shift arithmetic right | 751 |
| shls | $imm/%cl | %reg/mem | shift left | 756 |
| shrs | $imm/%cl | %reg/mem | shift right | 751 |
| subs | $imm/%reg | %reg/mem | subtract | 612 |
| subs | mem | %reg | subtract | 612 |
| tests | $imm/%reg | %reg/mem | test bits | 676 |
| tests | mem | %reg | test bits | 676 |
| xors | $imm/%reg | %reg/mem | bit-wise exclusive or | 747 |
| xors | mem | %reg | bit-wise exclusive or | 747 |
| s = b, w, l, q; w = l, q
| ||||
| program flow control:
| |||
| opcode | location | action | page |
| call | label | call function | 546 |
| ja | label | jump above (unsigned) | 683 |
| jae | label | jump above/equal (unsigned) | 683 |
| jb | label | jump below (unsigned) | 683 |
| jbe | label | jump below/equal (unsigned) | 683 |
| je | label | jump equal | 679 |
| jg | label | jump greater than (signed) | 686 |
| jge | label | jump greater than/equal (signed) | 686 |
| jl | label | jump less than (signed) | 686 |
| jle | label | jump less than/equal (signed) | 686 |
| jmp | label | jump | 691 |
| jne | label | jump not equal | 679 |
| jno | label | jump no overflow | 679 |
| jcc | label | jump on condition codes | 679 |
| leave | undo stack frame | 580 | |
| ret | return from function | 583 | |
| syscall | call kernel function | 587 | |
| cc = condition codes
| |||
| register direct: | The data value is located in a CPU register. |
|
| syntax: name of the register with a “%” prefix. |
|
| example: movl %eax, %ebx |
| immediate data: | The data value is located immediately after the instruction. Source operand only. |
|
| syntax: data value with a “$” prefix. |
|
| example: movl $0xabcd1234, %ebx |
| base register plus offset: | The data value is located in memory. The address of the memory location is the sum of a value in a base register plus an offset value. |
|
| syntax: use the name of the register with parentheses around the name and the offset value immediately before the left parenthesis. |
|
| example: movl $0xaabbccdd, 12(%eax) |
| rip-relative: | The target is a memory address determined by adding an offset to the current address in the rip register. |
|
| syntax: a programmer-defined label |
|
| example: je somePlace |
(§12.2) Write a program in assembly language that
prompts the user to enter a number in binary,
reads the user input into a char array,
converts the string of characters in the char array into a decimal integer stored in a local int variable, and
calls printf to display the int.
Your program should use the writeStr function from Exercise 11-3 to display the user prompt. And it should use the readStr function from Exercise 11-4 or 11-6 to read the user’s input.
Your program should read the user’s input into the local char array, then perform the conversion using the stored characters. Do not do the conversion as the characters are entered by the user.
Your program does not need to check for user errors. You can assume that the user will enter only ones and zeros. And you can assume that the user will not enter more than 32 bits. (Be careful when you test your program.)
(§12.2) Write a program in assembly language that allows the user to enter a decimal integer then displays it in binary.
Your program should convert the decimal integer into the corresponding C-style text string of ones and zeros, then use the writeStr function from Exercise 11-3 to display the text string.
This program will require some careful planning in order to get the bits to print in the correct order.
(§12.3) Write a function, mul16, in assembly language that takes two 16-bit integers as arguments and returns the 32-bit product of the argument. Write a main driver function to test mul16. You may use printf and scanf in the main function for the user interface.
Hint: Notice that most of the numbers in this problem are 16-bit unsigned integers. Read the man pages for printf and scanf. In particular, the ”u” flag character is used to indicate a short (16-bit) int.
(§12.4) Write a function, div32, in assembly language that implements the C / operation. The function takes two 32-bit integers as arguments and returns the 32-bit quotient of the first argument divided by the second. Write a main driver function to test div32. You may use printf and scanf in the main function for the user interface.
(§12.4) Write a function, mod32, in assembly language that implements the C % operation. The function takes two 32-bit integers as arguments and returns the 32-bit quotient of the first argument divided by the second. Write a main driver function to test mod32. You may use printf and scanf in the main function for the user interface.
(§12.4) Write a function in assembly language, decimal2uint, that takes two arguments: a pointer to a char, and a pointer to an unsigned int.
The function assumes that the first argument points to a C-style text string that contains only numeric characters representing an unsigned decimal integer. It computes the binary value of the integer and stores the result at the location where the second argument points. It returns zero.
Write a program that demonstrates the correctness of decimal2uint. Your program will allocate a char array, call readStr (from Exercise 11-4 or 11-5) to get a decimal integer from the user, and call decimal2uint to convert the text string to binary format. Then it adds an integer to the user’s input integer and uses printf to display the result.
Hint: Start with the program from Exercise 12-1. Rewrite it so that the conversion from the text string to the binary number is performed by a function. Then modify the function so that it performs a decimal conversion instead of binary.
(§12.4) Write a function in assembly language, uint2dec, that takes two arguments: a pointer to a char, and an unsigned int.
The function assumes that the first argument points to a char array that is large enough to hold a text string that represents the largest possible 32-bit unsigned integer in decimal. It computes the characters that represent the integer (the second argument) and stores this representation as a C-style text string where the first argument points. It returns zero.
Write an assembly language program that demonstrates the correctness of uint2dec. Your program will allocate one char array, call readStr (from Exercise 11-4) or 11-6 to get a decimal integer from the user, and call decimal2uint (from Exercise 12-6) to convert the text string to binary format. It should add a constant integer to this converted value. Then it calls uint2dec to convert the sum to its corresponding text string, storing the string in the char array.
Hint: Start with the program from Exercise 10-6. Rewrite it so that the conversion from the binary number to the text string is performed by a function. Then modify the function so that it performs a decimal conversion instead of binary.
(§12.3) Modify the program in Exercise 12-7 so that it deals with signed ints. Hint: Write the function decimal2sint, which will call decimal2uint, and write the function sint2dec, which will call uint2dec.