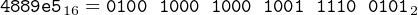
We are now ready to look more closely at the instructions that control the CPU. This will only be an introduction to the topic. We will examine the most common operations — assignment, addition, and subtraction. Additional operations will be described in subsequent chapters.
Each assembly language instruction must be translated into its corresponding machine code, including the locations of any data it manipulates. It is the bit pattern of the machine code that directs the activities of the control unit.
The goal here is to show you that a computer performs its operations based on bit patterns. As you read through this material, keep in mind that even though this material is quite tedious, the operations are very simple. Fortunately, instruction execution is very fast, so lots of meaningful work can be done by the computer.
The C/C++ assignment operator, “=”, causes the expression on the right-hand side of the operator to be evaluated and the result to be associated with the variable that is named on the left-hand side. Subsequent uses of the variable name in the program will evaluate to this same value. For example,
will assign the integer 123 to the variable x. If x is later used in an expression, the value assigned to x will be used in evaluating the expression. For example, the expression
would evaluate to 246.
This assumes that the expression on the right-hand side evaluates to the same data type as the variable on the left-hand side. If not, some automatic type casting may occur, or the compiler may indicate an error. We ignore the issue of data type for now and will discuss it at several points when appropriate. For now, we are working with arbitrary bit patterns that have no meaning as “data.”
We now explore what assignment means at the assembly language level. The variable declaration,
causes memory to be allocated and the location of that memory to be given the name “x.” That is, other parts of the program can refer to the memory location where the value of x is stored by using the name “x.” The type name in the declaration, int, tells the compiler how many bytes to allocate and the code used to represent the data stored at this location. The int type uses the two’s complement code. The assignment statement,
sets the bit pattern in the location named x to 0x0000007b, the two’s complement code for the integer 123. The assignment statement
sets the bit pattern in the location named, x to 0xffffff85, the two’s complement code for the integer -123.
Let us consider the simplest case where
That is, we will consider a program that simply sets a bit pattern in a CPU register. A C program to do this is shown in Listing 9.1.
The register modifier “advises” the compiler to use a CPU register for the integer variable named “x.” And the notation 0xabcd1234 means that abcd1234 is written in hexadecimal. (Recall that hexadecimal is used as a compact notation for representing bit patterns.) When the C program in Listing 9.1 is compiled into its assembly language equivalent with no optimization:
The C assignment operation is implemented with the mov instruction. For example, in Listing 9.1,
is implemented with
on line 13 in Listing 9.2. We can see that the compiler chose to use the ebx register as the x variable.
The mov instruction has an “l” (“ell”, not “one”) appended to it to indicate that the operand size is 32
bits. This is redundant because the register named as an operand, ebx, is 32 bits, but it is the
required syntax. The Intel syntax does not include this redundancy. If we consider the Intel
syntax:
| Intel® Syntax |
| mov | esi, -1412623820 |
we see the three other differences noted in Section 7.2.2 (page 509):
These differences are specific to the assembler program being used and are not relevant to the behavior of the CPU. The assembler program will translate the assembly language instruction into the correct machine language code.
The instructions on lines 14 – 17 implement the call to the printf function. One reason for the call to the printf function is to prevent the compiler from eliminating the assignment statement during its optimization of this function. Yes, even with the -O0 option the compiler does some optimization.
Compare the prologue with that of the null program in Listing 7.4 on page 512. Notice that the prologue
of this function includes saving the contents of a register and an adjustment to keep the stack pointer aligned on a sixteen-byte memory address boundary. However, the epilogue:
differs. In the epilogue, we need to restore the stack pointer, and restore any registers we saved on the stack, before restoring the calling function’s base pointer.
You may wonder why the gcc compiler assigns the constant -1412623820 to the variable, while the C version of the program assigns 0xabcd1234. The answer is that they are the same values. The first is expressed in decimal and the second in hexadecimal. We discussed the equivalence of decimal and hexadecimal in Section 2.2 (page 23), and we discussed signed decimal integers in Section 3.3 (page 87).
In Listing 9.3 we show the essential assembly language required to implement the C program from Listing 9.1.
Compare Listing 9.3 to the general pattern in Listing 8.13 on page 587. Note that the single instruction,
is the only “data processing” performed by this function. From this comparison, you can see that this assembly language statement implements the two C statements:
Like the compiler (Listing 9.2), we are using the ebx register as our variable. We can use the registers in Table 6.4 (page 469) as variables, except the stack pointer, %rsp, which has special uses. The “%” prefix tells the assembler that these are names of registers, hence in the CPU and not labels on memory locations.
Let us look more closely at the program in Listing 9.3. I used an editor to enter the code then assembled and linked it. Since it does not produce a display on the screen, I used gdb to observe the changes in the registers.
When using gdb to examine programs written in assembly language, another variant of the break command may be helpful. The version of gdb I used for this book skips over the function prologue. To cause gdb to break at the first instruction of a function, the following form should be used.
My typing is boldface.
$ gdb assignment2
I use the li command to list enough of the program to see where I should set the first breakpoint.
(gdb) br 13
I set the breakpoint on the instruction that implements the assignment operation.
(gdb) run
I run the program, it breaks at the first breakpoint, and I can display the registers that interest me.
(gdb) i r rbx rip
I use the i r (info registers) command to display the contents of the register that is used for the variable. The value in the rip register (the instruction pointer) is 0x4004d1.
(gdb) si
Next I use the single instruction (si) command to execute one instruction.
(gdb) i r rbx rip
Now I can see that the value, 0xabcd1234, has been assigned to the variable. Notice that the rip register has changed from 0x4004d1 to 0x4004d6. This tells us that the instruction that was just executed (movl $0xabcd1234, %ebx) is 0x4004d6 - 0x4004d1 = 5 bytes long.
(gdb) cont
Finally, I use the continue command (cont) to run the program out to its end.
(gdb) q
$
And, of course, I have to tell gdb to quit.
The assembly language instruction to perform binary addition is quite simple:
|
| adds | source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
destination += source
For example, the instruction
adds the 64-bit value in the rax register to the 64-bit value in the rdx register, leaving the rax register intact. The instruction
adds the 16-bit value in the dx register to the 16-bit value in the r10w register, leaving the entire rdx register and the high-order 48 bits of the r10 register intact.
In the Intel syntax, the size of the data is determined by the operand, so the size character (b, w, l, or q)
is not appended to the instruction. (And the order of the operands is reversed.)
| Intel® Syntax |
| add | destination, source |
We saw in Chapter 3 that addition may cause carry or overflow. Carry and overflow are recorded in the 64-bit rflags register. The CF is bit number zero, and the OF is bit number eleven (numbering from right to left). Whenever an add instruction is executed both bits are set as shown in Algorithm 9.1.
If the values being added represent unsigned ints, CF indicates whether the result fits within the operand size or not. If the values represent signed ints, OF indicates whether the result fits within the operand size or not. If the size of the operands is less than 64 bits and the operation produces a carry and/or an overflow, this is not propagated up through the next bits in the destination operand. The carry and overflow conditions are simply recorded in the corresponding bits in the rflags register.
For example, if we consider the initial conditions
would produce
would produce
The assembly language instruction to perform binary subtraction is
|
| subs | source, destination | |
where s denotes the size of the operand:
| s | meaning | number of bits |
| b | byte | 8 |
| w | word | 16 |
| l | longword | 32 |
| q | quadword | 64 |
destination -= source
For example, the instruction
subtracts the 32-bit value in the eax register from the 32-bit value in the edx register. The instruction
subtracts the 8-bit value in the dh register from the 8-bit value in the ah register.
In the Intel syntax, the size of the data is determined by the operand, so the size character (b, w, or l) is
not appended to the instruction. (And the order of the operands is reversed.)
| Intel® Syntax |
| sub | destination, source |
Subtraction also affects the CF and the OF. Whenever a sub instruction is executed both bits are set as shown in Algorithm 9.2.
Just as with addition, if the values being subtracted represent unsigned ints, CF indicates whether there was a borrow from beyond the operand size or not. If the values represent signed ints, OF indicates whether the result fits within the operand size or not. If the size of the operands is less than 64 bits and the operation produces a carry and/or an overflow, this is not propagated up through the next bits in the destination operand. The carry and overflow conditions are simply recorded in the corresponding bits in the rflags register.
For example, if we consider the initial conditions
would produce
would produce
A simple program given in Listing 9.4 illustrates both addition and subtraction in C.
Unfortunately, this program can give incorrect results:
The assembly language generated by gcc is shown in Listing 9.5 with comments added.
We see that a rather simple C statement:
must be broken down into distinct steps at the assembly language level:
Similarly, the C statement:
is broken down into the distinct steps:
It is easy to see that the compiler did not generate the most efficient code. (This was compiled with no optimization.)
An important lesson here is that writing complex statements in high-level programming languages does not improve efficiency. The statements are ultimately broken down into simple steps. See Exercise 9.3 for a comparison.
We have seen that the computations performed by both these C statements can produce overflow. Table 9.1 shows how the variables (and CF and OF) change as we walk through the code in the program of Listing 9.4. There are two runs of the program using the input values above.
| statement | w | x | y | z | CF | OF |
| scanf(); | 0x3b9aca00 | 0x77359400 | ???????? | ???????? | ? | ? |
| y = w + x; | 0x3b9aca00 | 0x77359400 | 0xb2d05e00 | ???????? | 0 | 0 |
| z = w - x; | 0x3b9aca00 | 0x77359400 | 0xb2d05e00 | 0xc4653600 | 1 | 0 |
| scanf(); | 0xc4653600 | 0x77359400 | ???????? | ???????? | ? | ? |
| y = w + x; | 0xc4653600 | 0x77359400 | 0x3b9aca00 | ???????? | 0 | 0 |
| z = w - x; | 0xc4653600 | 0x77359400 | 0x3b9aca00 | 0x4d2fa200 | 0 | 1 |
Listing 9.6 shows an assembly language program that performs the same operations as the C program in Listing 9.4 but uses the jno (jump if no overflow) instruction to check for overflow. These checks are easy in assembly language. They add very little to the execution time of the program, because most of the time only the conditional jumps are executed, and the jumps do not take place.
This section provides only a very brief glimpse of the machine code for the x86 architecture. The goal here is to provide you with a taste of what machine code looks like and thus emphasize that the computer is really controlled by groups of bit settings. The vast majority of computer professionals never need to know the machine code for the computer they are working with. For a complete description you will need to consult the manufacturer’s documentation.
Let us consider for a moment how we might design a set of machine instructions for a simple four-function computer. Our proposed computer can add, subtract, multiply, and divide. And we will suppose that it has 1 MB of memory. Each instruction must encode the following information for the control unit:
We will ignore the problem of getting data into the computer for this example, but we will certainly want to be able to move data from location to location in our computer. So we will have five operations:
Thus, if we want our computer to be able to add a value stored in one memory location to the value at another we need 3 + 20 + 20 = 43 bits to encode the instruction. Question: how many bits would be required if we wanted a design that would allow us to add two values stored in memory and store the sum at a third location?
Our silly design falls far short of practicality. The instructions themselves take too much memory, and we have allowed for only a very limited number of operations on the data. This was a more serious problem in the early days of computer design because memory was very expensive. The result was that computer designers came up with some clever ways to encode the necessary information into very few bits.
The design of the x86 processors is a very good example of this cleverness. Intel has paid particular attention to backwards compatibility as their designs have evolved. Thus, we see the remnants of the earlier designs — when memory was very expensive — in the latest Intel processors. The more common instructions generally take fewer bytes of memory. As newer, more complex features have been added, they generally take more bytes.
Computer design took a different turn in the 1980s. Memory had become much cheaper and CPUs had become much faster. This led to designs where all the instructions are the same size — 32 bits being very common these days.
We now turn our attention to the machine code that is produced by the assembler. Recall that it is the machine code that is actually executed by the control unit in the CPU. That is, the computer is controlled by bit patterns that are loaded into the instruction register in the CPU.
Programmers seldom need to know what the machine code is for any given assembly language instruction. The actual instruction depends upon the operation to be performed, the location(s) of the data to operate on, and the size of the data. Even when writing in assembly language, the programmer uses mnemonic names to specify each of these, and the assembler program translates them into the proper machine code instruction. So you do not need to memorize machine code. However, learning how assembly language instructions translate to machine code is important for learning how a computer actually works. And knowing how to “hand assemble” an instruction using a manual can help you find obscure bugs.
Most assemblers can provide the programmer with a listing file, which shows the machine code for each instruction. The assembly listing option for the gnu assembler is -al. For example, the “program” in Listing 9.7 contains some instructions that we will assemble and study to illustrate how to read machine language from a listing file.
The command to assemble the source file in Listing 9.7 and create a listing file is
The first column is the line number of the original source. You should recognize the right-hand two-thirds of the listing as the assembly language source. We will focus our attention on the second and third columns on the left-hand side.
The values in the first column are displayed in decimal, while the values in the second and third columns are in hexadecimal.
The function itself starts on line 8 with the label “main.” Since there is nothing else on this line in the source file, it does not occupy any memory in the program.
The first entry in the second column — 0000 — occurs at line 9. It shows the memory location relative to the beginning of the function. Since the source code on line 8 has only a label, the instruction on line 9 is the first one in this function. Furthermore, the label on line 8 applies to (relative) memory location 0000. The label allows other parts of the program to refer to this memory location by name. In particular, since the label, main, is declared as a .globl, functions in other files linked to this one can refer to this memory location. It effectively names this function as the main function.
The entry in the third column on line 9 is 55. It is the machine code at relative location 0000. That is, byte number 0000 in this function is set to the bit pattern 5516. Following the line across, we can see that this is the machine code corresponding to the instruction
Since the first instruction occupies one byte of memory, the second instruction will start in byte number 0001 (the second byte from the beginning). From the assembly listing file (Figure 9.1) we see that the machine code for
is the bit pattern
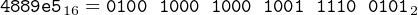 |
This instruction occupies three bytes. Thus, the third instruction in this function begins at the fifth byte — relative location 0004. Continuing to line 30, the last instruction in the program
is a one-byte instruction. It is the sixtieth byte in the function and is located at relative location 003b with the bit pattern,
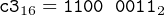 |
So you can use the -al option for the as assembler to produce an assembler listing, which will show you exactly what the bit patterns are for each instruction and which bytes, relative to the beginning of the function, are set to these patterns.
Instructions in the X86-64 architecture can be from one to fifteen bytes in length. Each byte falls into one of several categories:
The general placement of these bytes is shown in Figure 9.2.
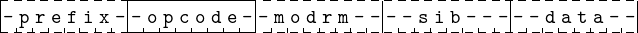
In order for an instruction to use the 64-bit features the x86-64 architecture uses a prefix byte, a REX prefix, placed immediately before the primary instruction. The assembler recognizes when a REX prefix is required and inserts it automatically; the programmer does not need to explicitly specify it. However, the assembler may give an error message that implies it is the responsibility of the programmer to insert a REX prefix. For example, when attempting to use
the assembler gave the error message:
REX prefixes are a byproduct of maintaining backward compatibility. The x86-32 architecture has only 8 general purpose registers, so it is sufficient to have only three bits in an instruction to specify any register. There are 16 general purpose registers in the x86-64 architecture, so four bits are required to specify a register. Some instructions involve up to three registers, thus there must be a place for three more bits to specify all the registers. Rather than change the register-specifying patterns in the Opcode, ModRM, and SIB bytes, the CPU designers decided to use the REX.R, REX.X, and REX.B bits in the REX prefix byte as the high-order bits for specifying registers. This provides the necessary three bits for register specification. A fourth bit in the REX prefix, the REX.W bit, is set to 1 when the operand is 64 bits. For all other operand sizes — 8, 16, or 32 bits — REX.W is set to 0. The format of the REX prefix byte is shown in Figure 9.3.
The format of a ModRM byte is shown in Figure 9.4.
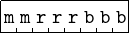
When one operand uses the base register plus offset addressing mode, that register is specified by the 3-bit bbb register field, and the other register is specified by the rrr register field. Table 9.2 shows the meaning of the 2-bit mm field.
| mm | meaning |
| 00 | memory operand; address in register specified by bbb |
| 01 | memory operand; address in register specified by bbb plus 8-bit offset |
| 10 | memory operand; address in register specified by bbb plus 16-bit offset |
| 11 | register operand; register specified by bbb |
If mm = 11 both operands are register direct and are specified by the two register fields, bbb and rrr. If mm = 00 the bbb register contains the memory address of one of the operands. The bbb register contains a base address for the other two values of mm. 01 means that an 8-bit offset, and 10 a 16-bit offset, is added to the base address to obtain the memory address. The offset is stored as part of the instruction.
The meaning of the register fields is shown in Table 9.3. For 64-bit mode, the REX bit column is explained in Section 9.3.3.
| REX | register | register | ||
| bit | field | names | ||
| 0 | 0 | 0 | 0 | rax, eax, ax, al |
| 0 | 0 | 0 | 1 | rcx, ecx, cx, cl |
| 0 | 0 | 1 | 0 | rdx, edx, dx, dl |
| 0 | 0 | 1 | 1 | rbx, ebx, bx, bl |
| 0 | 1 | 0 | 0 | rsp, esp, sp, spl, ah |
| 0 | 1 | 0 | 1 | rbp, ebp, bp, bpl, ch |
| 0 | 1 | 1 | 0 | rsi, esi, si, sil, dh |
| 0 | 1 | 1 | 1 | rdi, edi, di, dil, bh |
| 1 | 0 | 0 | 0 | r8, r8d, r8w, r8b |
| 1 | 0 | 0 | 1 | r9, r9d, r9w, r9b |
| 1 | 0 | 1 | 0 | r10, r10d, r10w, r10b |
| 1 | 0 | 1 | 1 | r11, r11d, r11w, r11b |
| 1 | 1 | 0 | 0 | r12, r12d, r12w, r12b |
| 1 | 1 | 0 | 1 | r13, r13d, r13w, r13b |
| 1 | 1 | 1 | 0 | r14, r14d, r14w, r14b |
| 1 | 1 | 1 | 1 | r15, r15d, r15w, r15b |
Notes:
The format of an SIB byte is shown in Figure 9.5.
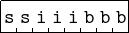
An SIB byte is required to implement the indexed addressing mode (see Section 13.1, page 799). The memory address is given by multiplying the value in the index register by the scale factor and adding this to the address in the base register. There can also be a offset, which is added to this sum.
We next consider the instruction on line 10 of Figure 9.1:
This instruction copies all eight bytes from the rsp register to the rbp register. It starts with a REX Prefix, followed by two bytes for the instruction itself. The general format of the instruction for moving data from one register to another is shown in Figure 9.6.

The REX Prefix is followed by the opcode, then an ModRM byte.
The opcode includes a “w” bit. This bit is 0 for 8-bit moves and 1 for all other sizes. The instruction operates on a 64-bit value, so w = 1 in the opcode (8916).
The 112 in the mod field of the ModRM byte shows that both the source and destination register numbers are encoded in this byte. The src field shows the source and the dst field shows the destination.
From Table 9.3 we see that the source register is either rsp, esp, or sp, and the destination register is either rbp, ebp, or bp. (w = 1 rules out the 8-bit registers.) Since the REX.W bit in the REX Prefix is 1, the operand size is 64 bits. Thus, the instruction makes a copy of all 64 bits in the rsp register into the ebp register.
The second mov format covered here is moving immediate data to a register. Examples are given on lines 11 – 14 of Figure 9.1. The first operand (the source) is a literal — the value itself is stated. This value will be stored immediately after the instruction. Of course, the instruction must encode the fact that this operand is located at the address immediately following the instruction — the immediate data addressing mode. The destination operand is a register — the register direct addressing mode. The general format for the move immediate data to a register instruction is shown in Figure 9.7 in binary.
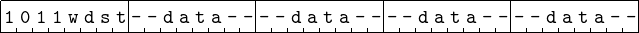
Consider the
instruction, the assembler determines that this is a mov instruction and the source operand is immediate data (due to the “$” character), so the first four bits of the opcode are 1011 (see Figure 9.7). Since the operand is not 8 bits, the “w” bit is 1. Next, the assembler figures out that the destination register is the r10 register. Looking this up on Table 9.3 (which is built into the assembler) shows that the remaining three bits are 010. Thus, the assembler generates the first byte of the instruction:
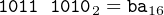 |
Since the operand size is 64 bits, the data value, 0x1234567890abcdef, is stored immediately (immediate addressing mode) after the instruction. Notice that the bytes seem to be stored backwards. That is, it looks like the assembler stored the 64-bit value 0xefcdab9078563412! Recall that the x86-64 architecture uses the little endian order for storing data in memory, so when the movl instruction copies four bytes from memory into a register, the byte at the lowest memory address is loaded into the least significant byte of the register, the byte at the next memory address is loaded into the next higher order byte of the register, etc. The assembler takes this into account for us and stores the immediate data in memory in little endian format.
The endian issue is irrelevant if you are always consistent with the size of the data item. However, if your algorithm changes data size, you need to be very aware of the endianess of the processor. For example, if you use a movl to store four bytes in memory, then four movbs to read them back into registers, you need to be aware of how they are physically stored in memory.
Finally, since this instruction operates on a 64-bit value, the instruction requires a REX Prefix. Referring to Figure 9.3 we see that the REX.W bit is 1, indicating the 64-bit size of the operands. And the REX.B bit is 1, which is used with the dst field to give the 4-bit number of the r10 register, 10102.
The add instruction has three different general formats. We present only a partial description here.
The format for adding an immediate value to a value in the rax, eax, ax, or al register is shown in Figure 9.8. The w bit is 0 for al and 1 for all others. The immediate data value must be the same size as the register to which it is added, except when adding to the rax register. Then the immediate data is 32 bits and is sign-extended to 64 bits before adding it to the value in the rax register. Note that this instruction is not used for the ah portion of the a register. For adding an immediate value to a value to the ah register or any of the other registers, the assembler program must use the instruction shown in Figure 9.9.

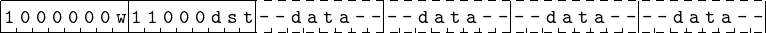
Notice that the instruction for adding to the a register (except the ah portion) is one byte shorter than when adding to the other registers (compare Figures 9.8 and 9.9). There is an historical reason for this. Early CPU designs had only one general purpose register. It was used as the “accumulator” for performing arithmetic. (Perhaps naming it the “a” register makes a little more sense.) As more general purpose registers were added to the designs, assembly language programmers tended to continue using the “accumulator” register more frequently than the others. And compiler writers continued this same pattern of register usage. Hence, the “a” register is used much more for addition in a program than the other registers, and making it a shorter instruction reduces memory usage and increases execution speed. The differences are generally irrelevant these days, but the x86 architecture has evolved in such a way to maintain backward compatibility.
The add instruction shown in Figure 9.10 is used when the data value is small enough to fit into one byte, but it is being added to a two-, four-, or eight-byte register. The value is sign-extended to a full 16-bit, 32-bit, or 64-bit value, respectively, inside the CPU before it is added to the register. Sign-extension consists of copying the high-order bit into each bit to the left until the full width is reached. For example, sign-extending 0x7f to 32 bits would give 0x0000007f; sign-extending 0x80 to 32 bits would give 0xffffff80. Notice that sign-extension preserves the signed decimal value of the bit pattern. (Review Section 3.3.)

An example of this is the instruction
Even though the value can be coded in only eight bits, the full 32 bits of the register may be affected by the addition. That is, the machine code is 83c105 (the data is coded in only one byte), but the CPU adds 0x00000005 to the rcx register. (Recall that this may produce different results than simply adding 0x05 to the cl portion of the ecx register.)
The format for adding a value in a register to a value in a register is shown in Figure 9.11. Again, the registers and size of data are specified by the bits w, src, and dst are given in Table 9.3, and “src” means “source” and “dst” means “destination.”
Let us look at the add instruction on line 17 in Figure 9.1:
This instruction adds the 32 bits from the ecx register to the 32 bits in the edx register, leaving the result in the edx register. From Table Table 9.3, w = 1, src = 001, and dst = 010. Thus the instruction is
00000001 110010102 = 01ca816
This summary shows the assembly language instructions introduced thus far in the book. The page number where the instruction is explained in more detail, which may be in a subsequent chapter, is also given. This book provides only an introduction to the usage of each instruction. You need to consult the manuals ([2] – [6], [14] – [18]) in order to learn all the possible uses of the instructions.
| data movement: | ||||
| opcode | source | destination | action | page |
| movs | $imm/%reg | %reg/mem | move | 506 |
| movs | mem | %reg | move | 506 |
| movsss | $imm/%reg | %reg/mem | move, sign extend | 693 |
| movzss | $imm/%reg | %reg/mem | move, zero extend | 693 |
| popw | %reg/mem | pop from stack | 566 | |
| pushw | $imm/%reg/mem | push onto stack | 566 | |
| s = b, w, l, q; w = l, q
| ||||
| arithmetic/logic:
| ||||
| opcode | source | destination | action | page |
| adds | $imm/%reg | %reg/mem | add | 607 |
| adds | mem | %reg | add | 607 |
| cmps | $imm/%reg | %reg/mem | compare | 676 |
| cmps | mem | %reg | compare | 676 |
| incs | %reg/mem | increment | 698 | |
| leaw | mem | %reg | load effective address | 579 |
| subs | $imm/%reg | %reg/mem | subtract | 612 |
| subs | mem | %reg | subtract | 612 |
| s = b, w, l, q; w = l, q
| ||||
| program flow control:
| |||
| opcode | location | action | page |
| call | label | call function | 546 |
| je | label | jump equal | 679 |
| jmp | label | jump | 691 |
| jne | label | jump not equal | 679 |
| jno | label | jump no overflow | 679 |
| leave | undo stack frame | 580 | |
| ret | return from function | 583 | |
| syscall | call kernel function | 587 | |
| register direct: | The data value is located in a CPU register. |
|
| syntax: name of the register with a “%” prefix. |
|
| example: movl %eax, %ebx |
| immediate data: | The data value is located immediately after the instruction. Source operand only. |
|
| syntax: data value with a “$” prefix. |
|
| example: movl $0xabcd1234, %ebx |
| base register plus offset: | The data value is located in memory. The address of the memory location is the sum of a value in a base register plus an offset value. |
|
| syntax: use the name of the register with parentheses around the name and the offset value immediately before the left parenthesis. |
|
| example: movl $0xaabbccdd, 12(%eax) |
(§9.1) Enter the assembly language program in Listing 9.3. Use gdb to single step through the program as shown in the book. Before executing each instruction, predict how the rax, rbp, and rsp registers will change. Also record the values in the rip and eflags registers as you single step through the program. How many bytes are there in each instruction?
(§9.2) Enter the C program in Listing 9.4. Using gdb, verify that the program works correctly, as shown in Table 9.1.
(§9.2) Modify the C program in Listing 9.4 such that the arithmetic operations are done in single steps:
Use the -S gcc option to generate the assembly language and compare it with the version in Listing 9.5.
(§9.2) Enter the assembly language program in Listing 9.6 and run it. Notice that it gives different results than the C version if there is overflow. Why is this? Modify the program so that it gives the same results as the C version but still gives an overflow warning.
(§9.3) Assemble each of the mov instructions in Listings 9.7 by hand. Check your answers with the assembly listing.
(§9.3) Assemble each of the add instructions in Listing 9.7 by hand. Check your answers with the assembly listing.
(§9.3) Assemble each of the following instructions by hand (on paper).
a) movl $0x89abcdef, %ecx b) movw $0xabcd, %ax c) movb $0x30, %al d) movb $0x31, %ah e) movq %r8, %r15 f) movb %r9b, %r10b g) movl %r11d, %r12d h) movq $0x7fffec9b2cf4, %rsi
and creating a listing file.
(§9.3) Assemble each of the following instructions by hand (on paper).
and creating a listing file.
(§9.3) Design an experiment that will allow you to determine what the machine code is for the
instruction, where “64-bit_register” is any of the general purpose registers. What is the general format of the instruction? Show your answer as a drawing similar to Figure 9.7. Which ones use a REX prefix? Hint: assemble with the -al option.
(§9.3) Design an experiment that will allow you to determine what the machine code is for the
instruction, where “64-bit_register” is any of the general purpose registers. What is the general format of the instruction? Show your answer as a drawing similar to Figure 9.7. Which ones use a REX prefix? Hint: assemble with the -al option.
(§9.3) Disassemble each of the machine instruction sequences by hand (on paper). (Find the corresponding assembly language instruction for each machine code instruction.) Notice that this is a much more difficult problem, because it is difficult to tell where one instruction ends and the next one begins. I have placed one machine instruction on each line to help you. Enter each of your assembly language programs into a source file and use the assembler to check your work.